Statistics Question With Answer

Attached are 5-year and 30-year Treasury Bond yields. Below the two datasets are not even – therefore, must set the dates covered by each series correctly!!!!

1.30-year rates – Weekly Data, 3/31/89 to 8/8/97

2.5-year rates – Weekly Data, 9/28/90 to 8/8/97

Be sure the data lines up correctly before starting your analysis.

Questions:
A. Run regressions on the 30-year and 5-year rates using only past information from the individual series.
B. Now run a Vector Auto-regression of the two interest rates together.
You should run a version for levels and a version for first differences.
A Vector Auto-regression involves running two regressions, one for each interest rate as a dependent variable, on the lags of both interest rates.
You can run a test for “Granger-causality” by examining whether any of the lags of the other interest rate help explain the current behavior of the first interest rate.

Solution:
The two time series data are represented by TBR_30Y and TBR_5Y. To find the number of lags that are significantly associated we have run the Auto Regression model with three lags using SPSS software.( SPSS à Time Series à Create Models…..)
The output of the analysis is given below.

From the above table we can see that the lag _1 is significantly associated as its corresponding significance value is less than 0.05. ( at 5% level of significance). We can also see that the other lags namely lag_2 and lag_3 are not significantly associated with the present value of the time series. Thus we can run a auto regressive model with lag_1 to get a reasonable model.
Thus the time series data TBR_30Y is run with auto regressive lag one and the results are given below.

From the above table we can see that the corresponding model is given by

That is in terms of the actual values we have

Since the R2 value for the corresponding model is 0.98 (98 %), we can conclude that the model with one lag considerably explains the variation in the dependent variable.

A similar analysis is run for the TBR_5Y values and their output is given below.

Here also we can see that lag_2 and lag_3 are not significant.

Thus the time series data TBR_5Y is run with auto regressive lag one and the results are given below.

From the above table we can see that the corresponding model is given by

That is in terms of the actual values we have

Since the R2 value for the corresponding model is 0.969 ( 96.9 %), we can conclude that the model with one lag considerably explains the variation in the dependent variable.

Vector Auto regression

The Vector auto regression is run with TBR_30Y as dependent variable and with its own two lags and with that of the TBR_5Y and its respective two lags as independent variables.
That is the dependent variable is taken as TBR_30Y and independent variables as TBR_30Y_LAG1, TBR_30Y_LAG2, TBR_5Y, TBR_5Y_LAG1, TBR_5Y_LAG2.
A regression analysis is carried out using SPSS and the results are given below.

Model Summary(b)

a Predictors: (Constant), TBR_5Y_LAG2, TBR_30Y_LAG1, TBR_5Y, TBR_30Y_LAG2, TBR_5Y_LAG1 b Dependent Variable: TBR_30Y

From the value of R2 ( 0.994 or 99.4 %) we see that the model well explains the variance in the dependent variable.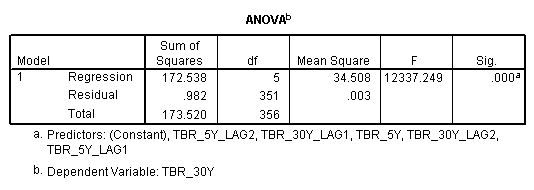

From the above ANOVA table we see that the model is significant at 5 % level.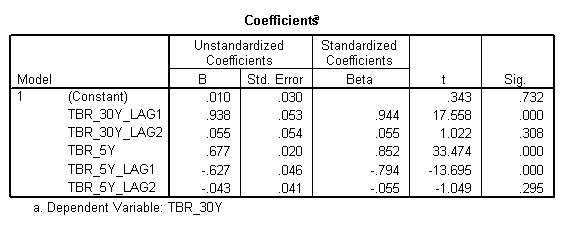

From the significance value of the coefficients we see that the second order lags are not contributing much to the model and that they can be dropped.( Their associated p- value is greater than 0.05)
Thus a model is again run with only lags of order one and the results are given below.

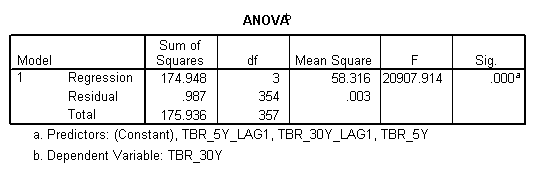
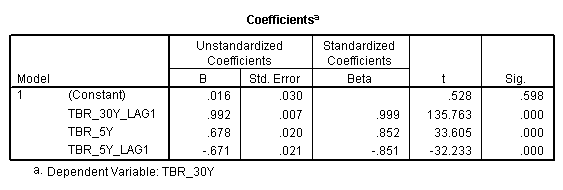
From the above tables we see that after dropping the lags of order two we get almost the same results with respect to R2 and significance of the model.
Thus the final model reduces to


A similar analysis is run for the TBR_5Y as dependent variable and with its own two lags and with that of the TBR_30Y and its respective two lags as independent variables.
That is the dependent variable is taken as TBR_5Y and independent variables as TBR_5Y_LAG1, TBR_5Y_LAG2, TBR_30Y, TBR_30Y_LAG1, TBR_30Y_LAG2.
A regression analysis is carried out using SPSS and the results are given below.

The output is given below.

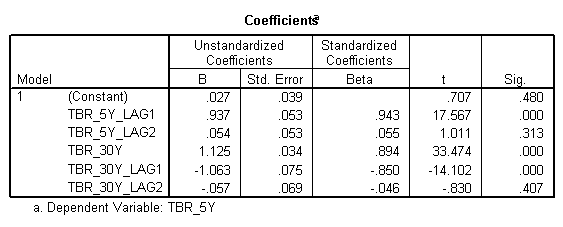
The pattern is similar to that of the TBR_Y30 and we as such can develop a model with only one lag.

Thus the final model and their output are given below.

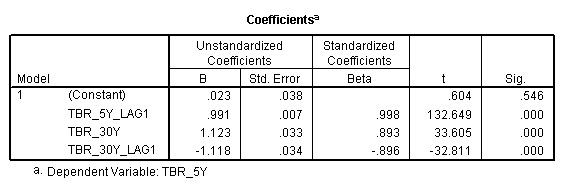
Thus the final model reduces to

-----END-----