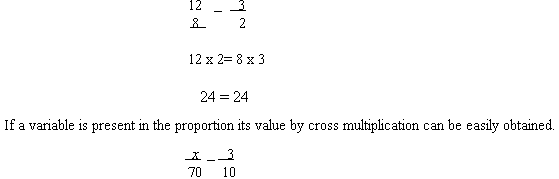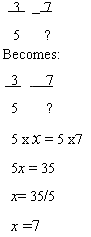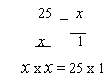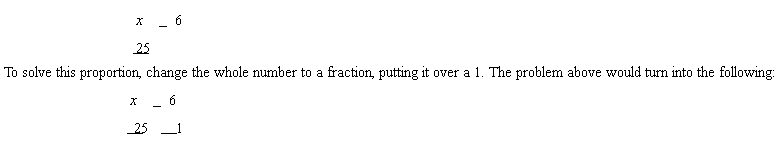Math Assignment Help With Proportions

Chapter 13. Proportions

13.1 Introduction: Two quantities having a same ratio are said to be in proportion. Proportion refers to the equality of two ratios. It can be written in two ways.

< a - c

< < b -d

for example if we write

1 pencil : 3 erasers

This means that for every pencil there are three erasers.

In simple words we can say “ a proportion is a comparison between two ratios”

Values in position of ‘b” and “c” are termed as means

Extremes: values in position of “a” and “d” are termed as Extremes.

13.2 Direct proportions: two quantities are said to be in direct proportion when the value of one of them increases or decreases with the other.

“α” is the sign used to represent direct proportion.

y α x

y=kx

k is the proportionality constant.

Examples

• The gravitational force acting on an object is directly proportional to its mass; the proportionality constant between mass and force is known as gravitational acceleration(g)

• Distance travelled by an object moving at a constant speed is proportional to the time spent in travelling, speed being the constant of proportionality.

• The circumference of a circle is proportional to its diameter, constant of proportionality is π.

13.3 Inverse proportionality: As stated above, two proportional variables are sometimes said to be directly proportional and two variables are said to be inversely proportional if one of the variables is directly proportional with the multiplicative inverse (reciprocal) of the other

y = k

- x

The constant can be found by multiplying x and y variable.

Inverse proportion means that as magnitude of one variable increases, the magnitude of another decreases, such that their product is always the same.

Example:

Time taken for a journey is inversely proportional to the speed of travel.

13.4 Exponential and Logarithmic Proportionality: A variable y is exponentially proportional to a variable x, if y is directly proportional to the exponential function of x.

y = k a^x

A variable y is logarithmically proportional to a variable x, if y is directly proportional to the logarithm of x.

y = k log_a(x)

13.5 Solving a proportion

13.5.1 Solving proportion without variable: By cross multiplying the numerator of the first ratio by the denominator of the second ratio and the denominator of the first ratio by the numerator of the second ratio.

If you encounter a proportion that has one of its means or extremes left blank, or uses another symbol such as a question mark you can treat it as if it was a variable. Or you can replace the question mark or blank space with a variable such as x. See the example below.

13.5.2 Solving a proportion with two variables:

A proportion with two of the same variable can be solved as shown below.

In these situations where a variable squared equals a number, you can do one of two things.

1. Find what number squared is equal to 25 using the perfect squares chart for reference.

(or)

2. Change the problem to x = square root of 25.

The resulting number from either method is equal to x and will be the answer.

13.5.3 When a whole number is in place of a fraction:

Take a look at the problem below, it doesn't have a fraction on one side.

And now it can be solved like any other proportion.

Email Based Homework Help in Proportions

To submit Proportions assignment click here.