Profit Maximisation
In this chapter we examine how a firm chooses its output level. We assume that all firms aim to maximise economic profits. The following equation is useful to analyse profits:
Economic profits = economic revenue – economic costs
When we discuss the level of costs associated with a particular output level we will assume that a firm is choosing the method of production that minimises its costs for that level of output. This is consistent with the assumption of maximising profits. Similarly, economists assume that firms will try to maximise revenue from the sale of whatever amount of output they have produced. Profit-maximising behaviour can be considered to have three elements:

- Choosing the production methods that minimise costs for a given level of output
- Choosing the selling price that maximises revenue for a given level of output
- Choosing the level of output that maximises profit.
The profit-maximising output can be found by equating marginal cost with marginal revenue
To find the profit-maximising output of a firm, we could differentiate profit with respect to output and find the output for which this is zero. That is, for profit maximisation we want:
d(profit)/ d(output) = 0
However, because:
profit = total revenue − total cost
this is equivalent to requiring:
d(total revenue) / d(output) = d(total cost) / d (output)
But, we know that:
d(total revenue)/d(output) = marginal revenue
and: d(total cost) / d(output) = marginal cost
Thus Profit maximisation requires output to be set at a level where marginal cost is equal to marginal revenue.
Consider the table below:
| Output | Price | Total | Total | Profit | Marginal | Marginal |
| Revenue | Cost | Revenue | Cost | |||
| 0 | - | - | 10.00 | (10.00) | - | - |
| 1 | 9.95 | 9.95 | 11.00 | (1.05) | 9.95 | 1.00 |
| 2 | 9.80 | 19.60 | 11.51 | 8.09 | 9.65 | 0.51 |
| 3 | 9.54 | 28.62 | 12.41 | 16.21 | 9.02 | 0.90 |
| 4 | 9.17 | 36.68 | 14.00 | 22.68 | 8.06 | 1.59 |
| 5 | 8.66 | 43.30 | 16.46 | 26.84 | 6.62 | 2.46 |
| 6 | 8.00 | 48.00 | 19.91 | 28.09 | 4.70 | 3.45 |
| 7 | 7.14 | 49.98 | 24.44 | 25.54 | 1.98 | 4.53 |
| 8 | 6.00 | 48.00 | 30.12 | 17.88 | (1.98) | 5.68 |
| 9 | 4.36 | 39.24 | 37.00 | 2.24 | (8.76) | 6.88 |
| 10 | - | - | 45.13 | (45.13) | (39.24) | 8.13 |
The profit-maximising output using the above table is six units (giving a profit of $28.09). If part units are possible, the profit-maximising output can be found mathematically to be just fewer than 5.9. Without allowing part units, we do not have marginal cost exactly equal to marginal revenue, but this is a minor qualification of the basic result. We certainly do have a case that satisfies the general rules. In general, if marginal revenue exceeds marginal cost, profits will be higher if output is expanded. If marginal cost exceeds marginal revenue, profits may be higher if output is reduced. In the example above, the profit-maximising level of output is six units. The marginal cost of the seventh unit exceeds the marginal revenue of the seventh units, so the firm’s profit would fall if it produced the seventh unit. However, the firm should not reduce its output; it should simply maintain production at six units of output
Profit-maximising output in the short run and the long run
We need to consider the precise profit-maximising conditions for a firm in different time periods. We will also take this opportunity to extend the profit-maximisation rule to cope with cases where profits are negative at all levels of output.
Profit-maximising output in the short run
In the short run, profit maximisation requires output to be set at a level where short-run marginal cost is equal to marginal revenue. However, if a company is not covering its variable costs it should shut down. A rational profit-maximising firm will never choose an output level that is expected to give a greater loss than the loss that would be incurred at zero output. Setting output to zero is the appropriate course of action if all non-zero levels of output would produce a loss greater than the amount of the fixed costs. We are assuming that costs are already being minimised, so that “cost cutting” exercises to improve the level of profits at positive output levels are not possible. To decide whether all non-zero output levels will produce a larger loss than the fixed costs, a firm needs only consider the positive output level Q at which MR = MC. We know that this is the profit-maximising, or loss-minimising, output. Having decided on this level of production, we now need to check whether the firm would in fact be better off with a zero output level.
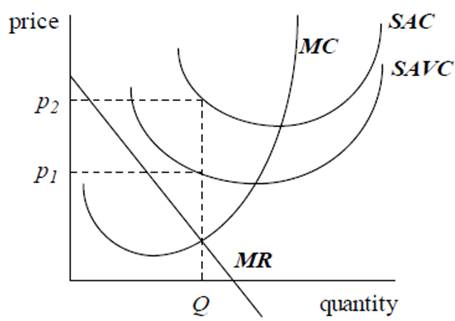
We want to compare total costs with total revenue to see which is greater. Equivalently, we can compare average costs with average revenue. If the average revenue is above p2 then the firm is covering its short-run average total costs and making a profit. It should continue to produce. If the average revenue is between p1 and p2, the firm is covering its short-run average variable costs, but not its short-run average fixed costs. It is therefore making a loss. However, the fixed costs will still be incurred whatever the output level. So, whether or not it is covering its fixed costs is irrelevant to the short-run decision as to what output level to set. So long as the price is above p1 the firm is able to cover its variable costs and also make a contribution towards its fixed costs. Thus the firm should stay in production in the short run. Although it is making a loss, the loss is smaller than it would be if output were zero. If the average revenue is less than p1 the firm should cut production to zero, i.e. shut down. p1 is therefore called the shutdown price.
Profit-maximising output in the long run
In the long run, profit maximisation requires output to be set at a level where long-run marginal cost is equal to marginal revenue. However, if a company is making an economic loss it should exit the industry. In the long run, even “fixed” factors of production can be varied. The firm's output decision is therefore as follows:
- Consider producing the level of output at which MR = LMC.
- If AR > LAC then the firm is making profits ⇒ continue production at this level.
- If AR < LAC then the firm is making losses. In the long run it has already had time to fully adjust its inputs. If it is still making losses it should quit production and exit the industry. Because of this, the price level equivalent to the LAC at the profit-maximising level of output is called the exit price.
where LMC = long-run marginal costs
AR = average revenue = total revenue divided by output = price
LAC = long-run average costs
MR = marginal revenue
The firm's output decisions are summarised in the table as below:
| Marginal condition | Check whether to produce | |
| Short-run decision | Choose output level where MR = SMC. | Produce this output unless price < SAVC. If it is, shut down. |
| Long-run decision | Choose output level where MR = LMC. | Produce this output unless price < LAC. If it is, exit industry. |
Note that “exit” is a long-run concept, depending upon (long-run average) total costs. In contrast, “shutdown” is a short-run concept depending upon (shortrun average) variable costs. The key distinguishing feature between long-run effects and short-run effects is that in the short run only some of the actions that may be taken in the long run are possible. In the short run, fixed factors are fixed, it is not possible to exit an industry, and so costs will be at least as high in the short run as in the long run.
Microeconomics | Microeconomics Help | Profit Maximisation | Microeconomics Costs | Marginal Revenue | Profit Maximization | Marginal Profit | Maximising Profit | Online tutoring


