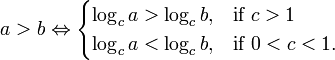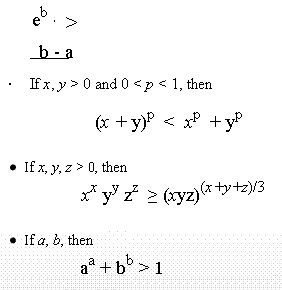Math Assignment Help With Inequalities And Trichotomy

CHAPTER 11 Inequalities and Trichotomy

11.1 Introduction: Inequalities between quantities or numbers or equations is the difference between them in respect of their magnitude or order.

• a < b means a is less than b
• a ≤ b means a is less than or equal to b
• a ≥ b means a is greater than or equal to b etc.
• a > b means a is greater than b etc.

In an inequality, you can add or subtract numbers from each side, with an equation.

You can also multiply or divide by a constant. However, if you multiply or divide by a negative number, the inequality sign is reversed.

Example: Solve 6(x + 4) < 8x + 21

6x + 24 < 8x + 21
-2x < -3
x > 3/2 (note: sign reversed because we divided by -2)

Inequalities can be used to describe the range of values of a variable.
E.g. 3 ≤ x < 10, means x is greater than or equal to 3 but less than 10.

11.2 Properties:

11.2.1 Trichotomy: The property states that

For any real numbers, a and b, only one of the following is true:

a < b

a = b

a > b

In set theory, trichotomy is defined as a property that a binary relation (<) has when all of its members satisfy exactly one of the relations listed above.

Strict inequality is an example of a trichotomous relation in this sense

11.2.2 Transitivity: The transitivity of inequalities states that

For any real numbers, a, b and c

If a > b & b > c, then a > c

If a < b & b < c, then a < c

If a > b & b = c, then a > c

If a < b & b = c, then a < c

11.2.3  Addition and Subtraction: This property deals with addition and subtraction. It states that:-

For any real numbers, a, b, c:

If a < b, then a + c < b + c and a − c < b − c

If a > b, then a + c > b + c and a − c > b − c

11.2.4  Multiplication and Division: This property deals with multiplication and division It states that:-

For any real numbers, a, b, c:

If c is positive and a < b, then ac < bc

If c is negative and a < b, then ac > bc

11.3 Rules to Solve Inequalities:

Here are some rules for solving inequalities and finding all of its solutions.

A solution of an inequality is a number which on being substituted for the variable makes the inequality a true statement.

Example: Consider the inequality

x – 4 > 3

Substitute any value, x = 9

The inequality becomes 9-2 > 5.

Thus, x = 9 is a solution of the inequality.

Substituting x = -2

(-2) – 4 > 3

-6 >3 which is not true.

 Thus x = -2 is NOT a solution of the inequality

Rule1. Add/subtract the same number on both sides.

Example: take any inequality

has the same solutions as the inequality

x – 6 +6 > 3 +6

Rule2. Switching sides and changing the orientation of the inequality sign.

Example: The inequality 5-x> 4

has the same solutions as the inequality

4 < 5 - x.

If you can notice the sides have been switched and turned the “>” into “<”

Rule 3. Multiply/divide by the same positive or negative number on both sides.

While multiplying or dividing by a negative number, remember to change the orientation.

Examples: Solve 4x > 6

Divide both sides by 4

Inequality becomes

x > 6/4

x>3/2

11.3.1 Special Cases - A variable in the denominator

For example consider the inequality

2/(x -1) >2

In this case we cannot multiply the right hand side by (x-1) because the value of x is unknown. Since x may be either positive or negative, its difficult to decide the inequality sign.

Step1. Equate the denominator to 0.

x-1 = 0

Step2: Assume inequality sign is an = sign

(2/x -1) = 2 so x = 2

Step3: Plot the points x = 1 and x = 2 on a number line with an open circle because the original equation included “ <”

Step4: check each region individually by arbitrarily picking a value within each region.

For example, the original inequality holds for x < 1, but not for x > 2 or 1 < x < 2.

11.4 Inequalities between means

There are many inequalities between means. For example, for any positive numbers a1, a2, …, an we have HM≤ GM ≤ AM ≤ QM,

11.5 Logarithms of inequalities

When manipulating inequalities it is sometimes useful to take the logarithm of both sides of the inequality. To do this the following result is needed.

11.6 Power inequalities:

Power inequality means inequalities which contain a^b type expressions where a and b are real positive numbers.

Examples

• If x > 0, then
  x ^x = (1/e)^1/e
  
  
• If x > 0, then
  
  (x^x)^x > x
• If x, y, z > 0, then
  
  (x + y)^z +(y + z)^x +(x+z)^y > 2
• For any real distinct numbers a and b
  
  e^(a+b)/2
  

Email Based Homework Help in Inequalities And Trichotomy

To submit Inequalities And Trichotomy assignment click here.