Eigenvectors Assignment Help

Introduction to Eigenvectors

Eigenvector acts on vector by changing both its magnitude and its direction. A matrix acts on an eigenvector by multiplying its magnitude by a factor. If the direction is unchanged and negative then it will positive and the direction will be reversed. These vectors are the eigenvectors of the matrix.

Eigenvectors Assignment Help By Online Tutoring and Guided Sessions at AssignmentHelp.Net

To each distinct eigenvalue of a matrix A there will be one eigenvector which are found by solving the appropriate set of homogenous equations. If i is an Eigenvalue then the corresponding eigenvector xi is the solution of

For example:

Find the Eigenvalues of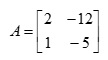

Solution:

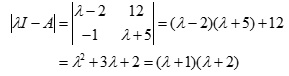
two eigenvalues: -1, - 2

Example

Theorem for Eigenvectors

• It corresponding to distinct (that is, different) eigenvalues are linearly independent.
• If is an eigen value of multiplicity k of an n n matrix A then the number of linearly independent eigenvectors of A associated with is given by m = n - r(A- I). Furthermore, 1 m k.