Binary Search Tree Assignment Help
A binary search tree (BST), also called an ordered or sorted binary tree, which has the following property for node-based binary tree data structure i.e.
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
1. Searching Algorithms
An algorithm is a step-by-step procedure to solve a problem by a computer in a given number of steps. The algorithm is written in human readable and understandable form. To search an element in a given array, it can be achieved by performing following algorithms:
- Linear search
- Binary search
- Hash search
- Binary search tree
We have gone through different terms such as binary tree, binary search, binary search tree at the time of exploring different searching algorithms. Let us understand them in a better way.
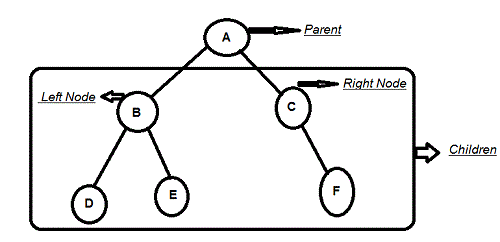
2. Binary Tree
Binary Tree is a special data structure used for storing data with a condition that each node can have a maximum of two children. A node in a binary tree is a data structure that has an element, and a reference to two other binary trees, typically called the left and right subtrees.
Figure: Representation of a Binary tree with nodes.
Need Assignment Help with Binary tree; contact our online chat support. More Tutorial for Binary tree
3. Binary Search
Binary Search is used to perform search in a sorted array. It performs the search by testing the middle element of the array. If it the middle element is too big, the process is repeated in the left half of the array, and the right half if the value of middle element is too small. By doing this the amount of space that needs to be searched is halved every time. The time taken to do so comes out to be O(log n).
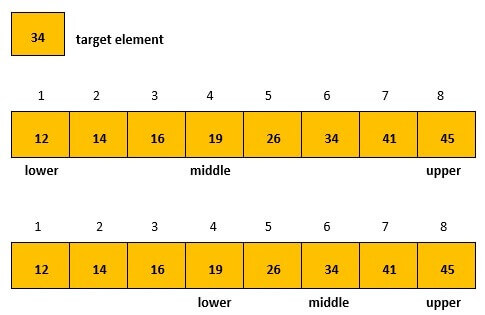
Figure: Performing binary search for a target element 34.
Our online Assignment Help tutors always ready for help you. More Tutorial for Binary Search
4. Binary Search Tree
Binary Search tree exhibits a special behavior i.e. the left child of the node should have value less than its parent's value and the right child of the node must have a value greater than its parent value. Searching in a binary tree is similar to searching in a hash table. It is usually slower if the tree is unbalanced to an extent.
Binary Search tree performs the search at the root. After searching the root, it goes down to the left subtree if the value of the element at root is too big and the right subtree if is too small. Then, repeat the process until we find the target element in the tree or the sub-tree we want is not present in the tree. The time taken to run binary search tree is O(log n) on average and O(n) in the worst case.
Tree resulting from the following insertions: 38, 13, 51, 10, 12, 40, 84, 25, 89, 37, 66, 95
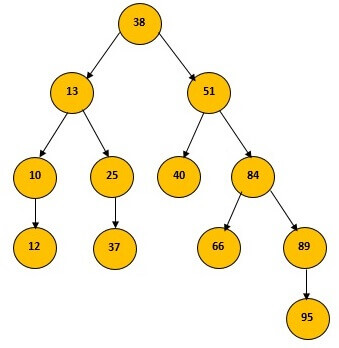
Figure: Performing insertion on binary search tree.
5. Binary Search Tree Algorithm
Now, let us understand the basic operations on Binary search tree with their algorithms.
5.1 Searching Algorithm
The binary tree search algorithm start searching for the target element from the root node. If the value of element found is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree of the tree. The algorithm is repeated for each of the node in the tree.
We will use the following procedure to search for a node with a given key or target value in a binary search tree.
Given a pointer to the root of the tree and a target element t,
TREE-SEARCH returns a pointer to a node with target element t if one exists; otherwise, it returns NIL.
TREE-SEARCH (x, t)
{`
1 if p = NIL or t = key[p]
2 then return p
3 if t < key[p]
4 then return TREE-SEARCH (left[p], t)
5 else return TREE-SEARCH (right[p], t)
`}
5.2 Insertion Algorithm
To insert an element in a binary search tree, first locate its proper location. The binary tree starts searching for the target node from the root node. If the value of the data is less than the key value, it searches for an empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.
To insert a new element or value v into a binary search tree T, we will use the procedure TREE-INSERT.
The procedure passes a node z for which key[z] = v, left[z] = NIL, and right[z] = NIL. It modifies T and some of the fields of z in such a way that z is inserted into an appropriate position in the tree.
TREE-INSERT (T, z)
{`
1 y ← NIL
2 x ← root[T]
3 while x ≠ NIL
4 do y ← x
5 if key[z] < key[x]
6 then x ← left[x]
7 else x ← right[x]
8 p[z] ← y
9 if y = NIL
10 then root[T]← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y]← z
`}
5.3 Deletion Algorithm
A given node z from a binary search tree can be deleted by taking as an argument a pointer to z.
The procedure consists of the following three cases.
- If z contains no children, its parent p[z] is modified to replace z with NIL as its child.
- If the node contains a single child, we interconnect z by making a new link between its child and its parent.
- If the node contains two children, we connect out z's successor y, which has no left child and replace the contents of z with the contents of y.
TREE-DELETE (T, z)
{`
1 if left[z] = NIL or right[z] = NIL
2 then y ← z
3 else y ← TREE-SUCCESSOR(z)
4 if left[y] ← NIL
5 then x ← left[y]
6 else x ← right[y]
7 if x ≠ NIL
8 then p[x] ← p[y]
9 if p[y] = NIL
10 then root[T] ← x
11 else if y = left[p[y]]
12 then left[p[y]] ← x
13 else right[p[y]] ← x
14 if y ≠ z
15 then key[z] ← key[y]
16 If y has other fields, copy them, too.
17 ⊳ return y
`}
5.4 Pre-order Traversal
In the Pre-order traversal method, the root node is visited first and then the left subtree and finally the right subtree.
{`1 void preorder(Node *root){
2 if(root){
3 printf("%d", root->data);
4 preorder(root->left);
5 preorder(root->right);
6 }
7 }
`}
5.5 In-order Traversal
In the In-order traversal method, the left subtree of the binary tree is visited first and then the root and later the right sub-tree. Always remember that every node may represent a subtree itself in a binary tree.
{`void inorder(Node *root){
if(root){
inorder(root->left);
printf("%d", root->data);
inorder(root->right);
}
}
`}
5.6 Post-order Traversal
In the Post-order traversal method, the root node is visited last. First, we traverse the left subtree and then the right subtree and finally the root node of the tree.
{`
1 void postorder(Node *root){
2 if(root){
3 postorder(root->left);
4 postorder(root->right);
5 printf("%d", root->data);
6 }
7 }
`}
6. Binary Search Tree in C++ Programming
To search a key element in a binary search tree.
{`
PROGRAM:
#include< iostream>
#include< conio.h>
#include< stdlib.h>
using namespace std;
void insert(int,int );
void delte(int);
void display(int);
int search(int);
int search1(int,int);
int tree[40],t=1,s,x,i;
main()
{
int ch,y;
for(i=1;i<40;i++)
tree[i]=-1;
while(1)
{
cout <<"1.INSERT AN ELEMENT\n2.DELETE AN ELEMENT\n3.DISPLAY ELEMENTS\n4.SEARCH AN ELEMENT\n5.EXIT\nEnter your choice:";
cin >> ch;
switch(ch)
{
case 1:
cout <<"Enter value of the element to insert in the tree";
cin >> ch;
insert(1,ch);
break;
case 2:
cout <<"Enter value of the element to delete from the tree";
cin >>x;
y=search(1);
if(y!=-1) delte(y);
else cout<<"no such element in tree";
break;
case 3:
display(1);
cout<<"\n";
for(int i=0;i<=32;i++)
cout << i;
cout <<"\n";
break;
case 4:
cout <<"enter the element to search:";
cin >> x;
y=search(1);
if(y == -1) cout <<"no such element in tree";
else cout << x << "is in" << y <<"position";
break;
case 5:
exit(0);
}
}
}
void insert(int s,int ch )
{
int x;
if(t==1)
{
tree[t++]=ch;
return;
}
x=search1(s,ch);
if(tree[x]>ch)
tree[2*x]=ch;
else
tree[2*x+1]=ch;
t++;
}
void delte(int x)
{
if( tree[2*x]==-1 && tree[2*x+1]==-1)
tree[x]=-1;
else if(tree[2*x]==-1)
{ tree[x]=tree[2*x+1];
tree[2*x+1]=-1;
}
else if(tree[2*x+1]==-1)
{ tree[x]=tree[2*x];
tree[2*x]=-1;
}
else
{
tree[x]=tree[2*x];
delte(2*x);
}
t--;
}
int search(int s)
{
if(t==1)
{
cout <<"no element in tree";
return -1;
}
if(tree[s]==-1)
return tree[s];
if(tree[s]>x)
search(2*s);
else if(tree[s]< x)
search(2*s+1);
else
return s;
}
void display(int s)
{
if(t==1)
{cout <<"no element in tree:";
return;}
for(int i=1;i<40;i++)
if(tree[i]==-1)
cout <<" ";
else cout << tree[i];
return ;
}
int search1(int s,int ch)
{
if(t==1)
{
cout <<"no element in tree";
return -1;
}
if(tree[s]==-1)
return s/2;
if(tree[s] > ch)
search1(2*s,ch);
else search1(2*s+1,ch);
}
`}
7. Binary Search Tree in JAVA Programming
Java Program to Implement a Binary Search Tree using Linked Lists.
{`
PROGRAM:
import java.util.Scanner;
class Node
{
Node left, right;
int data;
public Node(int n)
{
left = null;
right = null;
data = n;
}
}
class BST
{
private Node root;
public BST()
{
root = null;
}
public void insert(int data)
{
root = insert(root, data);
}
private Node insert(Node node, int data)
{
if (node == null)
node = new Node(data);
else
{
if (data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
}
return node;
}
public void inorder()
{
inorder(root);
}
private void inorder(Node r)
{
if (r != null)
{
inorder(r.left);
System.out.print(r.data +" ");
inorder(r.right);
}
}
public void preorder()
{
preorder(root);
}
private void preorder(Node r)
{
if (r != null)
{
System.out.print(r.data +" ");
preorder(r.left);
preorder(r.right);
}
}
public void postorder()
{
postorder(root);
}
private void postorder(Node r)
{
if (r != null)
{
postorder(r.left);
postorder(r.right);
System.out.print(r.data +" ");
}
}
}
public class LinkedListBST
{
public static void main(String[] args)
{
Scanner scan = new Scanner(System.in);
BST bst = new BST();
System.out.println("Linked List Binary Search Tree Test\n");
char ch;
do
{
System.out.println("Enter integer element to insert");
bst.insert( scan.nextInt() );
System.out.print("\nPost order : ");
bst.postorder();
System.out.print("\nPre order : ");
bst.preorder();
System.out.print("\nIn order : ");
bst.inorder();
System.out.println("\nDo you want to continue (Type y or n) \n");
ch = scan.next().charAt(0);
} while (ch == 'Y'|| ch == 'y');
}
}
`}
To submit Binary Search Tree Assignments Click here
The Assignment Help Services that we provide include: Binary Search Tree, Computer Programming, Data Structure, Trees Assignment Help, Binary Search Tree Project Help and Binary Search Tree Tutorials.
Binary Search Tree Assignment Help | Binary Search Tree Homework Help | Binary Search Tree Tutorials | Data Structure Online Help | Data Structure Course Help | Data Structure Problems Help | Data Structure Homework Help | Help With Programming Homework | Data Structure Programming Homework Help | Online Tutor | Complex Data Structure Programming Assignment Help | Homework Help | Tutor Online | Dissertation Help | Term Paper Help | Online Tutoring