Doppler Processing Assignment Help

Doppler Processing:

Mathematical observation:

Assume a target at a distance R and has a radial velocity component of Vr. The roundtrip

distance to target is 2R. This is equivalent to 2R/λ wavelengths or (2R/λ)2π = 4πR/λ

radians. If the phase of the transmitted signal is φo, then the phase of the received signal

is

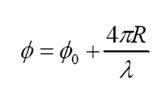
Alternatively, let the transmitted frequency be ft. The received signal can be represented

as sin(2 ( )) rec t R A = K πf t − t. The round-trip time tR is equal to 2R/c. With a radial

velocity of Vr the round-trip time is changing as R = R0 – Vrt. Thus, the received signal is

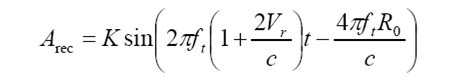
Thus, the received frequency changes by a factor 2ftVr/c = 2Vr/λ., which is the same as

before. The Nyquist criterion says that fmax = PRF/2, combining this with Equation (1),

results in

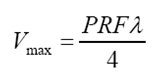
This is the maximum unambiguous velocity. Higher velocities cause velocity folding or

Doppler Processing Assignment Help Through Online Tutoring and Guided Sessions from AssignmentHelp.Net

Velocity aliases.

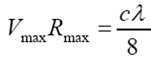
This summarizes the Doppler dilemma: a large Rmax implies a small Vmax and vice versa

Doppler process recognizing and dealing with range and velocity aliases

• On examining horizontal and vertical shapes of object. For example range-aliased incoming objects become skinny close-by objects. Incoming objects suspicious 3m – 150m wide, 130m – 6.2 km height.
• Then we examine reflectivity in conjunction with other factors,
• Changed PRF–real echoes will not change position, but aliases will. This is not always an option.
• Velocity folding causes a change in sign, which is relatively easy to spot if the Folding is within a larger region.