Operations Management Assignment Help

Scenario: You are the Senior Operations Manager at P&IC, Inc. that manufactures several models of personal computers and personal digital music players. You are faced with several production and inventory control dilemmas that need addressing. You must use the concepts of production and inventory control that have been studied in this course to address each problem.

1. Executives at P&IC and considering making a last production run of an older model of a computer model that is going to be eliminated within a year.

The unit production cost is $1,000 and the computer sells for $1,800. Computers that are not sold will be delivered to a discounted electronics vendor incurring transportation and handling cost of $180 per unit. The vendor pays P&IC $100 for each unsold computer. P&IC estimates a goodwill loss of $500 for any order short.

The demand pattern for the computer is exponential, with a PDF of

f (d)= e^-D/75 D

Operations Management Assignment Help Through Online Tutoring and Guided Sessions from AssignmentHelp.Net

a. What is the optimal production quantity to maximize expected profit? You must show your work clearly and completely to receive full credit.

b. What is the expected number of unsold computers? You must show your work clearly and completely to receive full credit.

Solution: I referred to Factory Physics 3^rd edition by Wallace J. Hopp and Mark L. Spearman

Page 95

Q*

f (d)=e^-D/75 - 1/Q^-D/P P =75

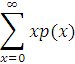
2. In one functional area of P&IC’s production facility, there is a three-station production line that produces a single model of computer. The computer visits Station 1, 2, 3 in that order. Station 1 has five identical machines with average processing times of 15 minutes per job. Station 2 has 12 identical machines with average processing times of 30 minutes per job. Station 3 has one machine with average processing time of 3 minutes per job.

Production system dynamics is often the method of choice when evaluating long-run production system performance. Assuming no variability (i.e., no process variability or flow variability in the production line), if the cycle time at the critical WIP level is 100 minutes, where does performance fall relative to the three general cases – the best case, the worst case and the practical worst case? Is there room for improvement? You must show your work clearly and completely to receive full credit.

Solution: I referred to Factory Physics 3^rd edition by Wallace J. Hopp and Mark L. Spearman

Page 235

5 machines 12 machines 1 machine

Station 2 Station 3

Station 1 has five identical machines with average processing times of 15 minutes per job.

Station 2 has 12 identical machines with average processing times of 30 minutes per job.

Station 3 has one machine with average processing time of 3 minutes per job.

W_o = r_b T_o

W_{o =} Critical WIP (work in process)

r_{b =} bottleneck rate of a line, defined as the rate of the station with the highest utilization.

T_o = raw process time

WIP=TH*CT

Critical WIP level cycle time = 100 minutes

The product runs into three stations production line

It goes through station 1->2->3 in that order.

At Station 1, five machines, the product stays for an average 15 minutes = 1/3 or .33 jobs per minute

At Station 2, 12 machines, the product stays for an average 30 minutes 4/10 = .4

At Station 3, 1 machine the product stays for an average of 3 minutes.

So the highest long term utilization rate R_b= 1/3 =.33

Stations 1 and 3 are bottlenecks with a capacity of 0.33 jobs per minute

The raw processing time is T₀ = 15+30+3 = 48

So, W₀ = r_b*T_o = 1/3 (48) 16 jobs per min

Best Case Performance

So, minimum cycle time will be,

CT _best (w) = 48, when w ≤ 16

= w / (1/3) when otherwise .33 w

Worst Case Performance:

The worst case cycle time for a given WIP

level, w, is given by,

CT_worst = wT₀ = w 48

The worst case throughput for a given WIP level, w, is given by,

TH_worst = 1=T₀ = 48 minutes

So minimum cycle time will be,

CT best (w) = 48, when w ≤ 1.6

= w/ (1/30) when otherwise that is 30 w otherwise

Worst Case Performance:

The worst case cycle time for a given WIP

level, w, is given by,

CT_worst = wT₀ = w 48

The worst case throughput for a given WIP level, w, is given by,

THworst = 1=T₀ = 48 minutes

Practical Worst Case Performance

The practical worst case (PWC)

(PWC) cycle time for a given WIP level, w, is given by,

CT_PWC = T₀ + (w -1)/ r_b = 48+ (1.6-1)/30 = 48.02

3. In different functional area at the P&IC facility at the facility that produces a model of digital music players, a production line staffed by three workers. Currently, the three workers have fixed assignments: each worker fastens a specific set of components onto the job and passes the job downstream on a rolling conveyor. The conveyor has capacity to allow a queue to build up in front of each worker. The bottleneck is in the middle station with a rate of 11 jobs per hour. The raw process time is 15 minutes. To improve the efficiency of the production line, management at P&IC is considering cross-training the workers to implement a flexible labor system.

Using the concepts of production system dynamics and assuming no process variability and flow variability, if the current throughput is 10.5 switches per hour with an average WIP level of five per jobs, how much potential do you think there is for a flexible labor system? You must show your work and discuss your reasoning clearly to receive full credit.

Solution:

Given:

The problem states: Three station production systems with each station assigned 1 worker per station.

The Bottleneck is Station number two with the station average process time r_b = 11 jobs per hour equals

60 minutes/11jobs per hour minutes = 5.5minutes, T_o = 15 minutes (=1/4 of a hour)

TH = 10.5 jobs per hour, WIP = 5 Jobs, CT = 5 jobs/10.5 jobs per hour

Raw process time is approx. ¼ hour less than the cycle time.

Now after implementing the flexible system, expected process variability will be reduced. Now current through put is TH = 10.5 per hour.

Hence the current average production turnaround time is = 5.7 minutes

We have seen the bottleneck time is 5.5 minutes. Hence there is always a chance to improve the throughput to 11 per hour to match the bottleneck time at least.

With WIP level 5 and throughput 10.5, the cycle time should be CT = W/TH = 5/10.5 = 28.57143 minutes which is quite high.

Hence, with the above analysis there is a lot of scope to go for flexible labor system as the current system of 5 WIP level is not acceptable for achieving the raw process time of 15 minutes.

4. At, yet another functional area within the P&IC production facility, there exists a two station production line where there is an intermediate buffer of finite capacity between the two stations. There is a single machine at each station. An unlimited supply of raw materials precedes Station 1. Therefore, the first station can always pulls in material. Also, the station 2 can always push material to finished goods. The buffer in between the two stations can hold only 10 jobs. Both machines take 20 minutes per job and have a squared coefficient of variation equal to 1.

Management at P&IC is contemplating setting the intermediate buffer size to one in order to reduce WIP. Also, assume management achieves their goals of reducing the CVs process at the stations to 0.25. Using the concepts of production system dynamics, what would be an upper bound on WIP inventory in the system? Also, compute an approximate upper bound on the total cycle time. Is this upper bound an acceptable cycle time?