Advance Finance Sample

Executive Summary

This report presents the financial analysis of a business expansion project Mainfreight New Zealand as presented in the case study. The financial analysis undertaken evaluates the case and NPV of the project if implemented today. The financial analysis considers the cash flows and NPV under different market scenarios. The financial analysis also considers the option of delaying the project by a year. The NPV and operating cash flow analysis reveal that project seems to be favourable if it is delayed by a year due to reduced uncertainty in the demand. The report also analyses the investment timing option using the decision tree framework and the Black Scholes model. However, both methods give different results.

1.0 Introduction

The financial analysis aims at enhancing decision making by offering an overview of the viability, stability, and profitability of business or project. This report presents a financial analysis for a project for the publicly listed company- Mainfreight. Mainfreight is a New Zealand based logistics and transport company that has a local as well as a global presence. The project was analysed in this report related to the piece of land owned by the company near Auckland International airport. Currently, the land has a warehouse facility that generates annual rents of $ 600,000. The case study outlines that that company is considering using the building for the expansion of its logistics business. The report offers an analysis evaluates and compares the financial impacts of using the building for the expansion of the logistics business as compared to its current usage. In this analysis, cash flow analysis, NPV analysis, decision tree analysis, and Black-Scholes Option Pricing (BSOP) model has been used to evaluate the different aspects of the project considered. The report also offers conclusions based on financial analysis.

2.0 Cash flows & NPV- if implemented today

This section offers a valuation of the project if implemented today using an NPV approach.The net present value (NPV) method of evaluating a project aims at analysing the present value of the future cash flows. The NPV of the project has been used as a basis to accept or reject the project. The project is considered to be favourable only if it results in the generation of positive NPV. According to the data provided in the case study, Mainfreight faces three possible demand scenarios based on market conditions – low, medium, and high demand scenarios. The cash flows and NPV of the project under these three scenarios are presented in table 1. A low demand scenario has a 30% probability of occurrence and generates annual revenue of $5 million. A medium demand scenario has a probability of 40% with an annual revenue of $8 million. And in case of high demand scenario that has a probability of 30% the annual revenues are $13 million. Net operating cash flows for all the three scenarios were calculated considering the fixed costs, variable costs, and depreciation. Firstly, the net operating profits after taxes (NOPAT)was calculated by using the following formula: -

Profit before = Cash inflows – Fixed costs – Variable costs – Depreciation

NOPAT = Profit before taxes – Taxes

The taxes were applied at 28% on the Profit before taxes and the net operating cash flows were determined by adding depreciation to NOPAT.

Table 1: Net operating cash flows & NPV based on demand variation

Table: Summary of Net NPV for investment today

The NPV for low demand scenario as well as the medium demand scenario is coming out be negative. Even the net NPV considering all three scenarios comes out to be negative i.e. -1.478 million. The NPV is positive only in case of high demand scenario.

To conclude, based on the present value of the net operating cash flows the project seems to unfeasible. If the company undertakes the building for the expansion of its logistics business with immediate effect it will result in net losses of $1.478 million.

3.0 Factors influencing investment’s success

The success of a project is a judgment by the rate of return offered by the project. The primary source of cash inflows is the annual revenues while the main drives of cash outflows is the fix and variable costs. Cost of capital is another important variable which measures the rate of return required by the project.Out of this fix cost can be ignored since it is constant each year. The impact of these variables i.e. annual revenues, variable costs, and cost of capital on investment outcomes can be determined by using sensitivity analysis. The investment profitability varies according to changes in the various factors. The sensitivity analysis aims at determining the impact of changes in various factors on the return of the investment. A sensitivity analysis over a range of values for annual revenues, variable costs, and cost of capital was conducted. The results of the sensitivity analysis are presented in figure 1 indicating the impact of changes in the different factors on the NPV of the project.

Figure 1: Sensitivity Analysis

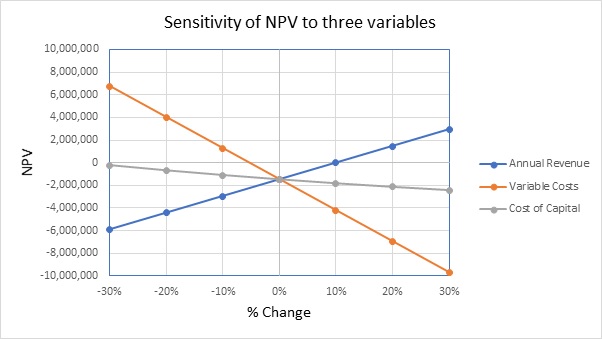
The graph reflects the variability in the NPV based on the percentage of changes in annual revenue, variable costs, and cost of capital. From the above graph, it can be observed that the variable costs have the most inclined gradient indicating its significant impact on the NPV of the project. On the other hand, the cost of capital has almost flatter curve. Thus, the variable costs are the most influential factor in determining the success of the investment. While the cost of capital has the least influence on the success of the investment.

4.0 NPV- in case the project is implemented a year later

In the given case scenario, it is being mentioned when the project is delayed for one year, the uncertainty related to the incremental demand scenario will last for one year only. It also assumes that once the business is established it will last forever. Thus, in such conditions, the firm will choose the project demand scenario based on the NPV of the cash flows. The operating cash flows and relative NPV for the project in different demand scenarios in case the project is undertaken after 1 year is presented in table 2.

Table 2: Cash flows & NPV

It can be observed from the above table that the NPV is positive only in the high demand scenario. Thus, the firm will undertake the high demand scenario as uncertainty related to demand does not exist. The net NPV, in this case, is calculated as below: -

Thus, in case the NPV is delayed for the project the firm is likely to undertake the project is the net NPV for the project in this scenario comes out to be $1.94 million.

5.0 Decision Tree analysis

The decision tree is a diagrammatic presentation used in facilitating capital investment decisions. The decision trees in financial analysis explain the value of the capital investment opportunities available with a firm. The decision tree helps in evaluating the different alternatives effectively. A decision tree is made up of nodes and branches, each brand represents an alternative Assignment of action while each note represents a chance event. Figure 2 represents a decision for the business expansion project implemented today.

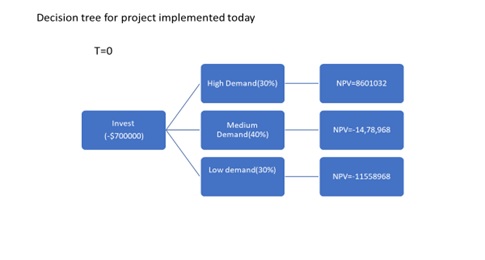
Figure 2: Decision tree for the project implemented today

From the above figure,it can be comprehended that the NPV for the project implemented today comes out to be -14,78,968. The negative NPV indicates that it is not feasible to implement the project today. The decision tree for the project delayed by 1 year is presented in Figure 3.

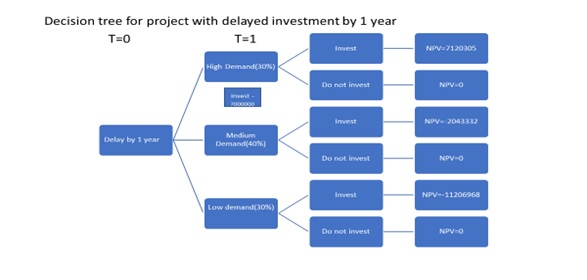
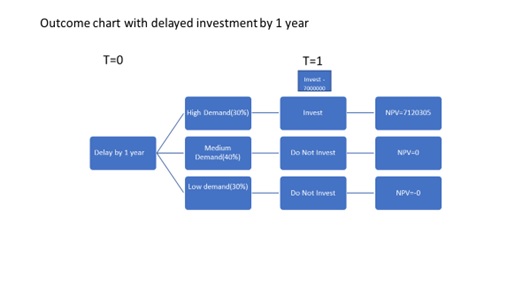
Figure 3: Decision tree for the project delayed by 1 year

The above figure indicates that if the project implementation is delayed by 1 year. shows the decision tree logic in case the project implementation is delayed by one year. After one year, the market demand conditions for the project will not face uncertainty and the project will be chosen in case of positive NPV. The decision tree indicates that in all three demand scenarios the firm has an option to invest or not invest. According to the outcomes chart, it is clear that the firm can undertake the project as the NPV is positive i.e. $7,120,305. The value of the investment timing option is calculated as below:-

NPV for project implemented today = -1478968

NPV for project delayed for 1 year = 7,120,305 * 30%= $2,136,092

NPV for project delayed for 1 year as of today = 2136092/1.1= 1941901

Value of timing = NPV for project delayed for 1 year as of today - NPV for project implemented today

= 1941901 +1478968 = $3,420,869

6.0 Black-Scholes option pricing model (BSOP)

To evaluate the project effectively an alternate model i.e. BSOP was also used. The Black Scholes model is widely used for the pricing of options contracts. The BSOP model is based on the concept that the price of the asset follows a Brownian motion with constant volatility. BSOP is based on the assumption that all the real options are European-style options that can be exercised at a particular time in the future. BSOP model estimates the value of options using the put-call parity. The model uses the following formula for determining the prices of call option:-

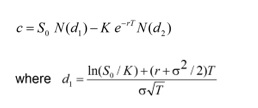
The model uses five important variables for determining the price of the option:-

• represents the underlying asset value, in the given case it is the present value of future operating cash flows arising from the project.
• is the exercise price paid for exercising the option
• is the risk-free rate which is normally taken as the return offered by a short-dated government bill.
• S is the volatility that is the risk attached to the project measured by the standard deviation.
• The time (t), which is the time, in years, that is left before the opportunity to exercise ends.

In the given case scenario, the cash flows change from -170% to 137% for the two given investment options.Variablity of the risk can be found using the distance from the mean. While using the BSOP model, the underlying price () based on the payoffs from high demand scenario regarding its probability (30%) and it comes out to be $3,850,992. The strike price (K)of the underlying asset is $7 million which is based on the initial set up costs. The risk-free interest rate is assumed to be 3% p.a. with one year. The BSOP call option price thus calculated is coming to be $1,146,351.

7.0 Conclusions

The above analysis yields significant insights related to the business expansion project for the Mainfreight New Zealand. It uses NPV approach based on cash flows as well as the investment timing According to the analysis, the project seems to unfeasible due to net negative NPV if it is undertaken today. It is not advisable to undertake the business expansion project as the NPV of cash flows are negative. However, the project can be considered with a delay of one year as there would be no uncertainty in the demand. And under the given case scenario the project has a positive NPV if it is delayed for a year. The analysis also reveal that the variable cost is the most influential factor to influence the success of the project. The analysis also uses two alternate methods of investment timing options- Decision tree and the Black-Scholes method

References

Damodaran, A. (2015).Applied corporate finance. Hoboken, New Jersey: Wiley.

Dixit, A., & Pindyck, Robert S. (1994).Investment under uncertainty. Princeton, N.J.: Princeton University Press.

Dikov, D. (2019) Decision trees in financial analysis. Retrieved from https://magnimetrics.com/decision-trees-financial-analysis/#:~:text=%20Decision%20Trees%20in%20Financial%20Analysis%20%201,evaluate%20a%20potential%20investment%20in%20a...%20More%20

Pettit, J. (2007). Strategic corporate finance : Applications in valuation and capital structure / Justin Pettit. (Wiley finance series). Hoboken, N.J.: John Wiley & Sons.

Ursone, P. (2015). How to calculate options prices and their greeks : Exploring the black scholes model from delta to vega / Pierino Ursone. (1.st ed., Wiley finance series).