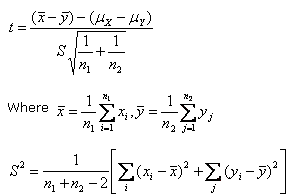Statistics Assignment Help With T Test For Difference Of Means
Suppose we want to test if two independent samples xi (i=1, 2, …….n1) and yj (j =1,2…………n2) of sizes n1 and n2 have been drawn from two normal populations with means μX and μY respectively.
Under the null hypothesis (H0) that the samples have been drawn from the normal populations with means μX and μY and under the assumption that the population variance are equal that is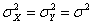 
, the statistic
Is an unbiased estimate of the common population variance σ2, follows Student’s t – distribution with (n1 + n2 – 2) degrees of freedom.
Email Based Homework Help in T Test For Difference Of Means
To submit T Test For Difference Of Means assignment click here.
Following are some of the topics in Exact Sampling Z Distribution in which we provide help:
- Exact Sampling Z Distribution
- Student T Distribution
- Derivation Of students T Distribution
- Fishers T Distribution
- T Test For Difference Of Means
- T Test For Testing Significance Of An Observed Sample Correlation Coefficient
- Testing The Significance Of An Observed Partial Correlation Coefficient
- Distribution Of Sample Correlation Coefficient
- Non Central T Distribution
Online Statistics Help | Statistics Math Help | Statistics probability help | Statistics help | College statistics help | Business statistics help | Elementary statistics help | Probability and statistics help | Statistics tutor | Statistic Homework help | Excel help | Mathematica help | Matlab help | MegaStat help | Minitab help | PHStat2 help | POM/QM help | R code and S-Plus help | SAS help | SPSS Help | Stata help | TDISK help | Tree Plan help | Online Tutoring
