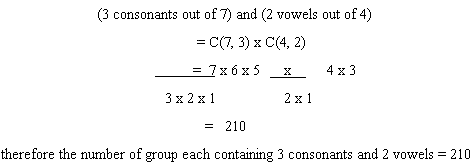Math Assignment Help With Practical Problems

11.3 Practical problems:

Example 1: In how many ways can a cricket team be chosen out of a batch of 20 players, if

i) there is no restriction in the selection;

ii) a particular player is always been chosen;

iii) a particular player is never chosen;

solution: i) the number of ways In which 11 players can be chosen out of 20 players;

here, n= 20 and r = 11

therefore,

C(20,11) = C(20, 20 – 11) = C(20, 9)

= 20!/ 9! (20 – 9) !

= 20x19x18x17x16x15x14x13x12/ 9x8x7x6x5x4x3x2x1

= 167960

ii) when a particular player is chosen always;

= C(19, 10) = C(19, 9)

= 19 x 18x17x16x15x14x13x12x11/ 9x8x7x6x5x4x3x2

= 21318

i) when a particular player is never chosen;

= C(19, 11) = (19, 2)

= 19 x 18/ 2

= 171

Example 2: In an examination, a candidate has to pass in each of the 5 subjects. In how many ways can he fail.

Solution: the student can fail by failing in 1 or 2 or 3 or 4 or 5 subjects out of 5 in each case.

Therefore, the total number of ways in which he can fail

= C(5, 1) + C(5 2) + C(5, 3) + C(5, 4) + C(5, 5)

= C(5, 1) + C(5 2) + C(5, 2) + C(5 1)

[using C(n, r) = C( n, n- r)]

= 5+10+10+5+1

= 31

Example 3: Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?

Solution: the number of ways of selecting

therefore the number of group each containing 3 consonants and 2 vowels = 210

To submit Practical Problems assignment click here.