OLS Regression with Dummy Variable in STATA
DUMMY VARIABLE REGRESSION IN STATA
EXAMPLE: The specification of our model assumes that the intercept and the slope coefficient on EDU are the same for all individuals. We may think that the effect of schooling on wages differs by a constant factor of proportionality for males and females, i.e.
that for males: WAGE = αM exp {`β1EDU + β2EX + β3EXSQ`} exp {`ε`}
While for females, WAGE = αF exp {`β1EDU + β2EX + β3EXSQ`} exp {`ε`}
Where αM and αF are differing factors of proportionality, β is the common return to schooling and ε is a random error term. Show that this implies that when the dependent variable LNWAGE rather than WAGE, males and females have different intercept terms but common slope coefficients β1 , β2, β3. To estimate these different intercepts, run the following regression
LNWAGE = α1 + α2FE + β1EDU + β2EX + β3EXSQ + ε
Interpret the estimates of α1 and α2 relating them to αM and αF above. Formulate and test the hypothesis (at 5% significance level) that there is no gender discrimination using your estimates of α1 and α2.
STATA Command for Dummy Variable Regression
In this part, we run the following regression using STATA; LNWAGE = α1 + α2FE + β1EDU + β2EX + β3EXSQ + ε
In this model, there is one additional term FE. It is a dummy variable which takes the value 1 for female and 0 for male. All other variables are same as in the previous model. The regression output and STATA commands used is given as under:
{`Regress LNWAGE EDU EX EXSQ FE`}
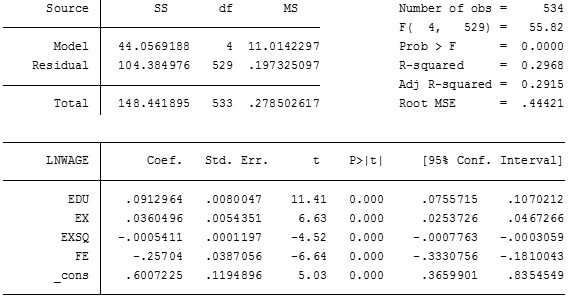
Interpretation of STATA Output for Dummy Variable Regression
The value of α1 is 0.6007225, which implies that on an average male earns a minimum hourly wage (with no experience and education) in logarithmic terms equal to 0.6007225. The value of α2 is -0.25704, which implies on an average female hourly wage earnings in logarithmic terms is 0.25704 lesser than males with same level of experience and education.
Conducting T-Test in STATA to Check Difference Between Mean of Two Groups
To test for difference between the mean values of the dependent variable based on different categories of the Dummy Variable we carry out t-test for difference between two means. Here in our example we can test the gender discrimination using ttest in stata. The STATA t-test output and STATA command for t-test used is as follows:
{`ttest LNWAGE,by (FE)`}
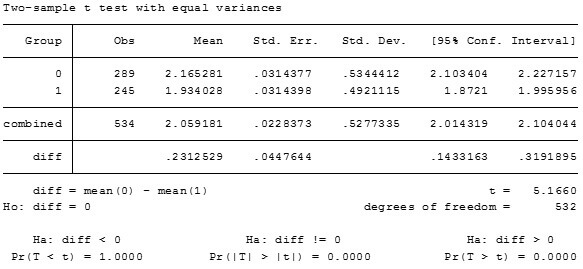
Interpretation of STATA output for t-test for difference between means
Since, t- statistic is greater than 2 in absolute value; we reject the null hypothesis that the difference in LNWAGE across gender is not statistically significant and thereby not rejecting the alternative hypothesis that the difference is statistically significant at 5% level of significance. Therefore, we conclude that the difference in LNWAGE of 0.25704 is statistically significant at 5% level of significance and women do receive statistically lower hourly wages than men based on the given sample.
