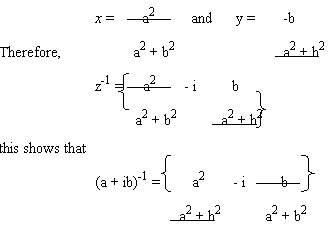Math Assignment Help With Multiplication properties

1.6.2 Multiplication properties:

Theorem1: (Closure property): If z1 and z2 ϵ C, then the product of two complex numbers is a complex number, i.e.

z1. z2 ϵ C

Proof: Let z1 = (a + ib)

And,

z2 = c + id

where

a, b, c, d ϵ R

therefore,

z1 . z2 = (a + ib) (c + id)

= (ac – bd) + i (ad + bc) ϵ C

As stated by the closure property of addition, subtraction and multiplication of real numbers (ac – bd) and (ad + bc) both are real numbers.

Hence,

(ac – bd) + i (ad + bc) ϵ C

Therefore,

z1 ϵ C ; z2 ϵ C z1. z2 ϵ C for all z1, z2 ϵ C

Theorem 2 :( Commutative Law): If z1, z2 ϵ C then,

z1z2 = z2z1

Proof: Let z1 = (a + ib)

And,

z2 = c + id

z1 z2 = (a + ib) (c + id)

= (ac – bd) + i (ad + bc)

= (ca – db) + i (da + cb)

= (c + id) (a + ib)

= z2 z1

Thus,

z1z2 = z2z1

Theorem3: (Associative law): If z1, z2, z3 ϵ C, then

(z1 z2) z3 = z1 (z2 z3)

Proof: Let z1 = a + ib

And,

z2 = c + id

z3 = e + if

(z1 z2) z3 = [(a + ib) (c + id)] (e + if)

= [(ac – bd) + i (ad + bc)] + (e +if)

= {(ac – bd) e – (ad + bc) f}+ i {(ac – bd)f + (ad +bc)e}

= (ace – bde – adf – bcf) + i (acf – bdf + ade + bce)

= {a (ce – df) – b (cf + de)} + i {a(cf + de) + b(ce – df)}

= (a + ib) {(ce – df) +i (cf +de)}

= z1 (z2 z3)

Thus,

(z1 z2) z3 = z1 (z2 z3)

Theorem4: (Multiplicative Inverse): For each z ϵ C, there exist a complex number denoted by z^-1 such that

z ^z-1 = z^-1 z = 0

Proof: z = a + ib ϵ C

And,

z ≠ 0

let z^-1 = (x + iy) ϵ C

Then,

z z^-1 = 1

(a + ib) (x + iy) = 1

(ax – by) + i(bx + ay) = 1 + i0

ax – by = 1

and

bx + ay = 0

Email Based Homework Help in Multiplication properties

To submit Multiplication properties assignment Click here.

Following are some of the topics in Complex Number in which we provide help: