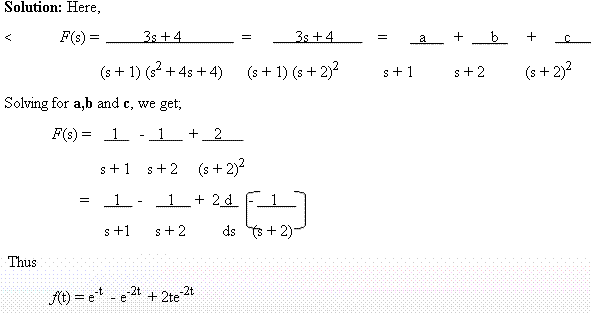Math Assignment Help With Inverse Transforms Of Rational Functions

4.8 Inverse Transforms of Rational Functions

Let F(s) be a rational function of s. Inverse Laplace transform of F(s).

Example:

i) If denominator of a function has distinct real roots:

F(s) = (s + 1) (s + 3) find f(t)

s (s + 2) (s + 8)

Solution:

F(s) = 3 + 1 + 35

16s 1(s + 2) 48(s + 8)

Thus,

F(t) = 3 + 1 e^-2t 35 e^-8t

Inverse Transforms Of Rational Functions Assignment Help Order Now

16 12 48

ii) Denominator of a function has distinct complex roots:

If F(s) = 4s + 3 find f(t)

s² + 2s + 5

<Solution: F(s) = 4 s + 1 - 1 2

(s + 1)² + 2² 2 (s + 1)² + 2²

Thus,

F(t) = 4e^-t cos(2t) – 1 e^-1 sin(2t)

iii) Denominator of a function has repeated real roots:

F(s) = 3s + 4 find f(t)

(s + 1) (s² + 4s+ 4)

$integration of rational functions$

Email Based Assignment Help in Inverse Transforms Of Rational Functions

To Schedule an Inverse Transforms Of Rational Functions tutoring session Live chat
To submit Inverse Transforms Of Rational Functions assignment click here.

Following are some of the topics in Rational Function in which we provide help:

Assignment Writing Help

Engineering Assignment Services

Do My Assignment Help

Write My Essay Services