Statistics Assignment Help With Independence Of Attributes

Two attributes A and B are said to be independent if there exists no relationship of any kind between them. If A and B are independent, we would expect

(i) The same proportion of A’s amongst B’s as amongst β’s,
(ii) The proportion of B’s amongst A’s is same as that amongst the α’s.

9.4.1 Criterion of independence:

If A and B are independent, then (i) gives

Which is (2). Similarly, starting from (2), we would arrive at (1).

It becomes easier to grasp the nature of the above relations if the frequencies are supposed to be grouped into a table with two rows and two columns as follows:

Attributes	A	α	Total
B	(AB)	(αB)	(B)
β	(Aβ)	(αβ)	(β)
Total	(A)	(α)	N

Second criterion of independence may be obtained in terms of the class frequencies of first order. (3) gives

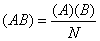
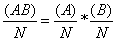
class frequencies

Which leads to the following important fundamental rule:

“if the attributes A and B are independent, the proportion of AB’s in the population is equal to the product of the proportions of A’s and B’s in the population.”

We may obtain a third criterion of independence in terms of second order class frequencies, as follows.

Email Based Homework Help in Independence Of Attributes

To submit Independence Of Attributes assignment click here.

Following are some of the topics in Theory of Attributes in which we provide help: