Statistics Assignment Help With Random Variable And Discrete Random Variable
If a random variable takes at most a countable number of values, it is called a discrete random variable. In other words, a real valued function defined on a discrete sample space is called a discrete random variable.
3.3.1 Probability mass function:
Suppose X is a one – dimensional discrete random variable taking at most a countably infinite number of values x1, x2……… with each possible outcome xi, we associate a number pi = P(X =xi) = p(xi), called the probability of xi. the number p(xi); I = 1, 2,…….. must satisfy the following conditions:
- (i) P(xi) ≥0
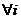
- (ii)
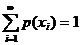
This function p is called the probability mass function of the random variable X and the set { xi, p(xi)} is called the probability distribution (p.d.) of the r.v. X.
3.3.2 Discrete distribution function:
Suppose there are a countable number of points x1, x2,……… and numbers p≥0, 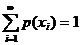. Such that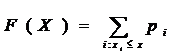 
For example if xi is just the integer i. F(x) is a “step function” having jump pi at I, and being constant between each pair of integers.
Email Based Homework Help in Discrete Random Variable
To submit Discrete Random Variable assignment click here.
