Statistics Assignment Help With Chebycheves Inequality
The role of standard deviation as a parameter to characterize variance is precisely interpreted by means of the well known Chebchev’s inequality.
Theorem:

If X is a random variable with mean μ and variance σ2, then for any positive number k, we have
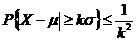
Or 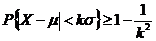
Proof:
When X is a continuous random variable. By definition
Email Based Homework Help in Chebycheves Inequality
To submit Chebycheves Inequality assignment click here.
Following are some of the topics in Mathematical Expectation And Generating Function in which we provide help:
- Mathematical Expectation And Generating Function
- Expectation Of A Function Of A Random Variable
- Addition Theorem Of Expectation
- Multiplication Theorem Of Expectation
- Expectation Of A Linear Combination Of Random Variable
- Correlation Coefficient
- Moments Of Bivariate Probability Distributions
- Conditional Expectation And Conditional Variance
Online Statistics Help | Statistics Math Help | Statistics probability help | Statistics help | College statistics help | Business statistics help| Elementary statistics help | Probability and statistics help | Statistics tutor | Statistic Homework help | Excel help | Mathematics help | Matlab help | MegaStat help |Minitab help | PHStat2 help | POM/QM help | R code and S-Plus help | SAS help | SPSS Help | Stata help | TDISK help | Tree Plan help | Online Tutoring



