Solved step by step with explanation - Circular Car Velocity Acceleration

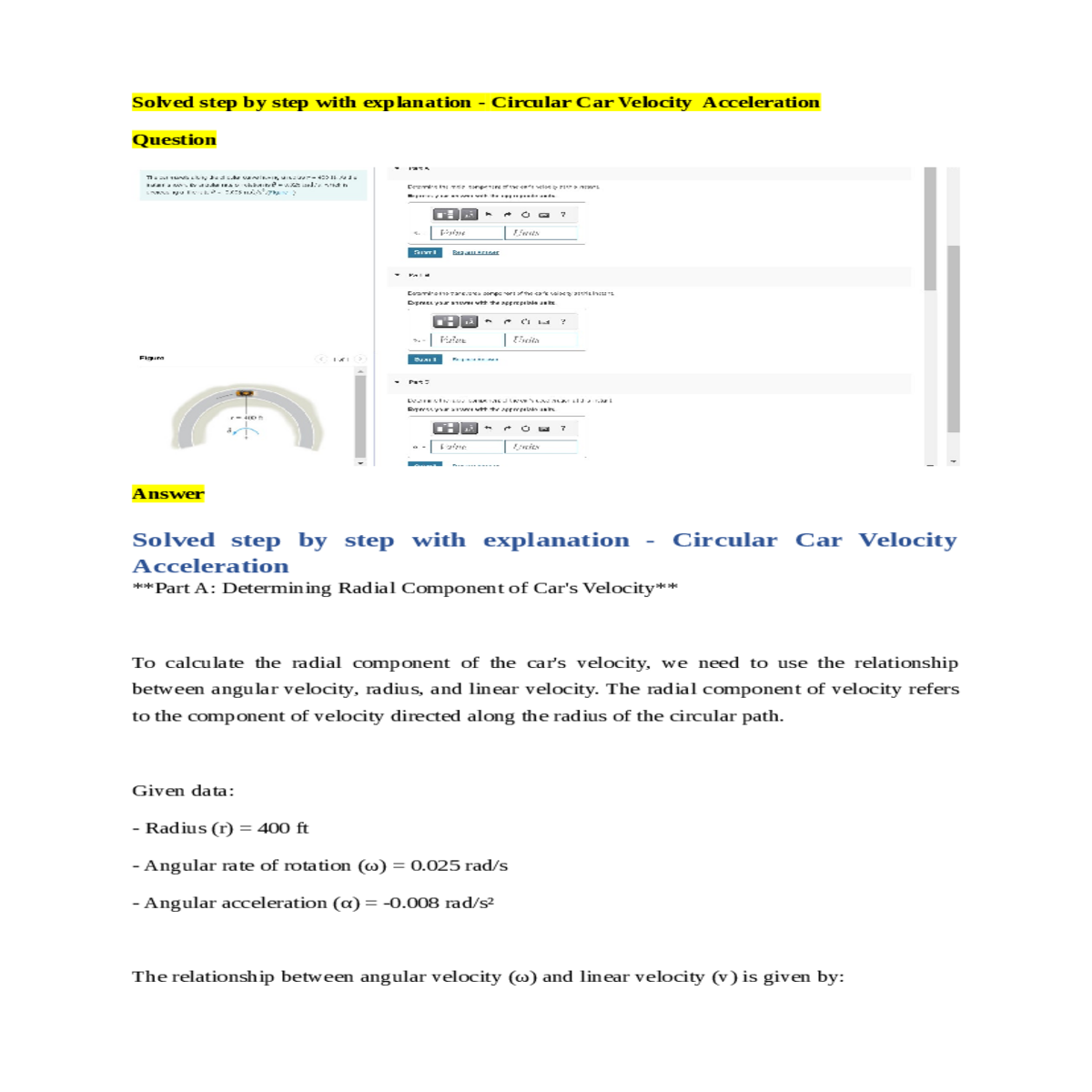
Question

Solved step by step with explanation - Circular Car Velocity Acceleration

Given data:

- Radius (r) = 400 ft

Differentiating this with respect to time to find the radial component of acceleration:

a_r = r * α

a_r = -3.2 ft/s²

2. Calculate the change in angular velocity:

θ = ω_initial * t + 0.5 * α * t²

θ = 0.025 rad/s * t + 0.5 * (-0.008 rad/s²) * t²

t = 6.25 s

5. Calculate the linear velocity at this instant:

**Part B: Determining Transverse Component of Car's Velocity**

The transverse component of the car's velocity is the component perpendicular to the radius, directed tangent to the circular path. This component can be calculated using the linear velocity and the angular velocity.

v_g = r * ω

Calculate the transverse component of the car's velocity:

The radial component of acceleration is the acceleration directed along the radius of the circular path. It can be calculated using the relationship between angular acceleration, radius, and linear acceleration.

Given data:

Calculate the radial component of the car's acceleration:

a_r = 400 ft * (-0.008 rad/s²)