{" "} Neighbourhood, Open Sets and Closed Set in R
Neighbourhood of a point
{`
A set A ⊂ R is called a neighbourhood (nbd) of a point a∈R if there exists an open interval ( a- ε, a +ε) for some ε> 0 such that
a ∈(a - ε,a + ε) ⊂ A
Equivalently A is nbd of a if ∃ an open interval I such that a ∈ I ⊂ A
Open sets
A set A ⊂ R is called an open set if it is neighbourhood of each of its points. Alternatively, a set A ⊂ R is called an open set if for each a ∈ A there exists some ε > 0 such that a ∈( a - ε,a + ε)⊂ A
A is not an open set if A is not a neighbourhood of even one of its points.
The set R of real numbers is a neighbourhood of all its points. For any real a, we have
a ∈ (a - ε,a + ε)⊂ R ∀ ε > 0
Thus the set R of real numbers is an open set.
The set Q of rational numbers is not a neighbourhood of any of its points because
a ∈ (a - ε, a + ε) ⊂ Q ∀ ε > 0
and any such interval contains rational as well as irrational points.
So set Q of rational numbers is not an open set.
The set of irrational numbers Q’ = R – Q is not a neighbourhood of any of its points as many interval around an irrational point will also contain rational points. So the set of irrational numbers Q’ is not an open set.
The open interval (a,b) is a neighborhood of all its points since
x ∈ (a, b) ⊂ (a, b) ∀ x ∈ (a, b)
So every open interval (a,b) is an open set. (-∞,a)and (b,∞)are also open sets.
The interval (a,b] is a neighbourhood of all its points except b since
b ∈ (b - ε, b + ε) ⊂ (a, b] ∀ ε > 0 (since b + ε > b)
Similarly [a,b) is neighbourhood of all its points except a and [a,b] is a nbd of all its points except a and b. Thus (a,b]; [a,b) and [a,b] are not open sets.
(-1/n,1/n) is a nbd of 0 ∀ n ∈ N
(-1/n,1/n) is an open set ∀ n ∈ N
`}
The set of natural numbers N, the set of whole numbers W, and,
the set of integers Z are not neighbourhood of any of their
points since N, W, Z cannot contain an interval. Thus the set
of natural numbers (N), set of whole numbers (W) and the set
of integers (Z) are not open sets. Any non-empty finite set
cannot be neighbourhood of any of its points as it cannot
contain an interval which has infinite number of points. So, a
finite set is not an open set. The null set ∅ is open in the
sense that there is no point in the null set ∅ of which it is
not a neighbourhood.
Some Theorems and their Proofs about Open Set
Theorem: The union of an arbitrary family of open sets is an open set.
{`
Proof : Let {Gλ: λ ∈ Λ} be an arbitrary family of open sets.
Let G = ⋃(λ∈Λ) Gλ. We have to show that G is an open set.
Let a be any element of G = ⋃(λ∈Λ) Gλ Then a ∈ Gλ for some λ ∈ Λ
Since Gλ is given to be open set so it is neighbourhood of each of its points and hence Gλ is neighbourhood of a.
Thus there exists some ε > 0 such that
a ∈ (a - ε, a + ε) ⊂ Gλ
As Gλ ⊂ ⋃(λ ∈ Λ) Gλ = G
Therefore, a ∈ (a - ε, a + ε) ⊂ G
⇒ G is nbd of a
`}
As a is any point of G therefore G is neighbourhood of each of its points and hence G is open set.
Theorem : The intersection of a finite number of open sets is an open set.
Proof : We first prove the intersection of two open sets G1 and G2 is an open set.{" "}
{`
Let a ∈ G1 ∩ G2 ⇒ a ∈ G1 and a ∈ G2
Since G1 and G2 are open sets therefore they are neighbourhoods of each of their points, in particular G1 and G2 are nbds of a. therefore there exists ε1 >0 and ε2 >0 such that
a ∈ (a-ε1,a + ε1 ) ⊂ G1
a ∈ (a - ε2,a + ε2 ) ⊂ G2
Let = Min{ε1,ε2 } so that ε ≤ ε1 and ε ≤ ε2. Thus
a ∈ (a - ε, a + ε) ⊂ (a-ε1, a + ε1 ) ⊂ G1
a ∈ (a - ε, a + ε) ⊂ (a - ε2, a + ε2 ) ⊂ G2
Therefore, a ∈ (a - ε, a + ε) ⊂ G1 ∩ G2
This implies that G_1∩G_2 is nbd of a
Since a was any point of G1 ∩ G2 therefore G1 ∩ G2 is nbd of each of its points and hence G1 ∩ G2 is open.
Now consider three open sets G1, G2, G3. Then,
G1 ∩ G2 ∩ G3= (G1 ∩ G2) ∩ G3
Now RHS is an intersection of two open sets.
G1 ∩ G2 and G3 is an open set and so G1 ∩ G2 ∩ G3 is an open set.
Proceeding like this if G1,G2,G3,…, Gn are finite number of open sets,then,
G1 ∩ G2 ∩ G3 ∩…∩ Gn is an open set.
Note: The intersection of an arbitrary family of open sets may not be an open set.
Theorem: The intersection of the family of all neighbourhoods of a point a is {a}.
Proof: Let {Na} be family of all neighbourhoods of a point a.
We have to show ⋂ Na = {a}
Let b ≠a and ε =|a - b| then,
(a - ε, a + ε) is nbd of a
and b ∈ (a - ε, a + ε) because if b ∈ (a - ε, a + ε) then a - ε < b < a + ε
or – ε < b - a < ε or |b-a| < ε which is a contradiction.
Since b ∈ (a - ε,a + ε) therefore b ∈ ∩ Na
So any b ≠ a results in b ∈ ∩ Na.
Hence ⋂ Na = {a}
Theorem: Every open set is a union of open intervals.
Proof: Let G be any open set. By definition for each x ∈ G,∃ some εx > 0 such that
x ∈ (x - εx ,x + εx ) ⊂ G
Thus G ⊂ ⋃(x∈G) (x - εx , x + εx ) ⊂ G
Hence G = ⋃(x∈G) (x - εx , x + εx )
Closed Set
A set A ⊂ R is called a closed set if and only if its complement A’ = R – A is an open set.
Thus A is closed ⇔ R-A is open
The set of real numbers R is closed set as R'= ∅ is an open set. Therefore the set of real numbers R is both open set and closed set.
The set of rational numbers Q is not closed set as Q’ the set of all irrational numbers is not an open set. Also the set of irrational numbers Q’ is not a closed set as (Q’)’ = Q (the set of rational numbers) is not an open set. So the set of all rational numbers Q and the set of all irrational numbers Q’ are both neither open set nor closed set.
Every closed interval [a,b] is a closed set as R - [a,b] = (-∞,a) ∪ (b,∞) being union of two open sets is an open set.
[a,b) is not a closed set as R - [a,b) = (-∞,a) ∪ [b,∞) is not open set as it is neighbourhood of all its points except b.
Similarly (a,b] and (a,b) are not closed sets.
The empty set Φ is closed set as Φ’ = R is open set. Therefore the null set Φ is both open set and closed set.
Some Theorems and their Proofs on Closed Set
Theorem: The intersection of an arbitrary family of closed sets is closed.
Proof: Let {Aλ ∶ λ ∈ Λ} be an arbitrary closed family of closed sets.
We have to show that
A= ⋂(λ∈Λ) Aλ is a closed set.
By De Morgan’s law
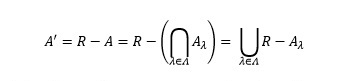Since each Aλ is closed therefore each R - Aλ is open set. Therefore A’ being arbitrary union of open sets is open set. Hence A is closed set.
Theorem: The union of a finite number of closed sets is a closed set.
Proof: Let A1, A2,…,An be n closed sets. Then R - A1,R - A2,…,R - An are open sets.
Therefore (R - A1) ∩ (R - A2)…∩ (R - An is an open set. (Since finite intersection of open sets is open set)
By De Morgan’s law
( R - A1 ) ∩ (R - A2 )…∩ (R - An ) = R - {A1 ∪ A2…∪ An }
Which implies R - {A1 ∪ A2…∪ An } is an open set.
Hence A1 ∪ A2…∪ An is closed.
`}
