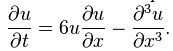Differential Equations Assignment Help

Introduction to Differential Equation:
A differential equation is any equation which contains an unknown function and one of its unknown derivatives. If only ordinary derivatives are present, then the equation is called an ordinary differential equation and if partial derivatives are involved, then the equation is called a partial differential equation. D.E play an extremely important role in applied math, engineering and physics.
Ordinary Differential Equations:
If y= f(x) is an unknown function, an equation which involves at least one derivatives of y w.r.t x is called an ordinary differential equation. The order of the D.E is the order of the highest derivative present in the equation and the degree of the D.E is the degree of the highest order derivative after clearing the fraction powers.
Example:
1. dy/dx=2x in this the Order =1, Degree =1
Solution of the differential equation of the first order and first degree:
The first order and first degree equation will be in the form
dy/dx = f(x,y)
Differential Equation of first order and first degree are classified in four types:
- Variables separable equation
- Homogeneous equation
- Exact equation
- Linear equation
Differential Equations Assignment Help By Online Tutoring and Guide Sessions at AssignmentHelp.Net
In the following examples, let u be an unknown function of x and c and are known constants.
In homogeneous equation
First-order linear constant coefficient ordinary differential equation:
du/dx = cu + x2
Second-order linear ordinary differential equation:
d2u/dx2 - x du/dx + u = 0
Second-order linear constant coefficient ordinary differential equation describing the harmonic oscillator:
d2u/dx2 + w2u = 0.
First-order nonlinear ordinary differential equation:
du/dx = u2 + 4.
Second-order nonlinear (due to sine function) ordinary differential equation describing the motion of a pendulum of length L:
L d2u/dx2 + g sin u = 0.
In these equation the unknown function u depends on two variables x and t or x and y.
Homogeneous first-order linear partial differential equation:
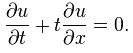
Homogeneous second-order linear constant coefficient partial differential equation of elliptic type, the Laplace equation:
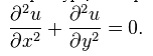
Third-order nonlinear partial differential equation, the Kortewegde Vries equation: