Valuation of Discount Bonds

THE VALUATION OF DEBT INSTRUMENTS

Present value analysis is used to determine the market price of debt instruments. A debt instrument is a written promise by a borrower to repay the owner of the debt-instrument, a specified amount in future. There are two kinds of debt instruments depending on their duration of maturity:

1. Short-term debt instruments such as Treasury bills, commercial paper and repurchase agreements. These short-term debt instruments are bought and sold at price determined in the money market.

2. Long-term debt instruments such as U.S. Treasury bonds and corporate bonds. These long-term debt instruments are traded at prices determined in the capital market.

Initially a debt instrument is first bought (by the lender) and issued (by a borrower) in the primary market. The debt instrument can also be resold in a secondary market.

A debt instrument can be such that it repays the future value in a single amount or such that it can repay the future amount in the form of several future payments.

Debt Instruments Sold on a Discount Basis: Discount Bonds

Many debt instruments-including Treasury bills, banker’s acceptances, and some forms of corporate bonds- do not pay interest directly. These debt instruments called as discount bonds are sold on a discount basis. This means that they are sold at a price that is less than their face value. Thus at maturity, the lender presents the discount bond to the borrower and the borrower pays him the face value.

For example, the face value of a Treasury bill is $100,000. This means that the U.S. Treasury promises to pay $10,000 to the owner of the Treasury bill when it matures – let’s say, in a year. These Treasury bills are sold through auction at a price that is less than their face value, (for example, $95000).

Thus, for these discount bonds the return to the owner of a discount bond is the difference between the face value collected at maturity and the purchase price.

Discount Yield and Yield of maturity

The yield on a Treasury bill (discount bond) is equal to the percentage annual return earned by the owner of the instrument.

The yield on a discount bond is measured by two methods:

1. Discount yield method
2. Yield to maturity.

The discount yield, which is frequently used to measure yields on Treasury bills, is defined as

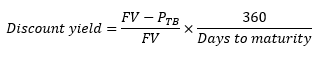
Where FV is the future value of the Treasury bill, or the face value. This face value represents the amount that will be paid when the bill matures-and PTB is the price paid for purchasing the Treasury bill. Suppose, a $10000 Treasury bill that matures in 365 days and was purchased for $9500 would have a discount yield of

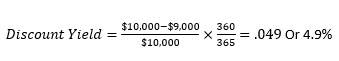
This discount yield formula in fact under-calculates the actual yield on a Treasury bill. This is because firstly this formula is based on a 360-day year, instead of the standard 365-day year. Secondly, the discount yield formula calculates the percentage return to the investor on the face value of the Treasury bill, [the term (FV-PTB)/FV], rather than its actual purchase price in the denominator [(FV-PTB)/PTB]. Since PTB is less than FV, the discount yield formula understates the actual yield on a Treasury bill.

A better method to calculate the yield of a discount bill is the yield to maturity. The yield to maturity is the interest rate at which the amount used to purchase the Treasury bill would have to be invested to grow to the face value paid at maturity.

For example: Consider the one-year, $10000 Treasury bill purchased for $9500. At what interest rate would one have to invest $9500 today to end up with $10000 at the end of one year? Thus, we need to calculate the value of rate of interest, i, that satisfies the following equation:

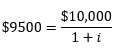
Solving this equation for i we get i= 0.053.

Thus, the yield to maturity on the Treasury bill is 5.3 percent. Notice that this yield to maturity is greater than the discount yield which proves that the discount yield understates the actual return on the discount bond.

Valuing Debt Instruments Sold on a Discount Basis.

In a discount bond, since the lender receives a fixed face value on maturity, the price at which any lender is willing to purchase a discount bond is based on the market interest rate.

• When the interest rate is low, the investor will willingly pay a relatively high price (and earn a relatively low yield) as the alternative investments will also give a low return.
• When the interest rate is high, the investor will pay relatively low price and earn a relatively high return.

The market interest rate is determined by the interaction of demand of loanable funds and supply of loanable funds. The demand of loanable funds comes from the borrowers while the suppliers of loanable funds are the lenders. At equilibrium, the demand for loanable funds is equal to the supply of loanable funds at the equilibrium market interest rate.

Given the scenario in figure 8.1, we can determine the present value of the Treasury bill-the amount a typical the amount a typical investor would be willing to give up today to receive the promised $10000 in one year. In particular, when the interest rate is 7 percent, the price of the Treasury bill (PTB) is the present value of the $10000 received one year in the future:

For example, the maximum price the seller of the Treasury bill (FV = $10,000) could obtain given the 7 percent market interest rate is PTB = $9345.79. At any higher price, investors would not purchase this discount bond since they could earn a higher return by investing their money in some alternative investment.

Changes in determinants of demand of loanable funds and/or supply of loanable funds- such as wealth, inflationary expectations, and tax rates-can shift demand or supply, resulting in changes in the interest rate. Any change in a determinant of demand or supply affects bond prices.

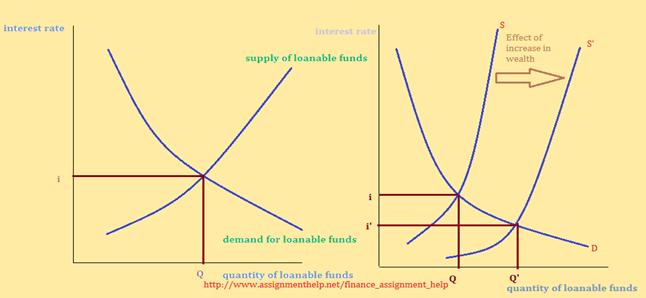
For example, what happens to bond prices if wealth increased?

The increase in wealth would increase lenders’ willingness to loan out funds, thus increasing the supply of loanable funds. In this case, equilibrium moves to a lower market interest rate. At a lower interest rate, the price of the Treasury bill rises to

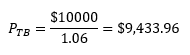
Thus the increase in wealth led to a decline in the interest rate, which in turn increased the price of the Treasury bill.

Thus, as the interest rate falls, the price of a debt instrument sold on a discount basis rises. There is an inverse relationship between the price of the discount bond and the market interest rate.