Quick Sort Assignment Help
1. What is Sorting Algorithm
Sorting algorithm arranges the elements of a collection in certain order. Sorting of elements is generally based on either lexicographic order or numeric order. The sorting should be done in efficient way so as to make the optimization task easy. And the output produced after sorting must satisfy this condition, “The Output should be only reordering of the input elements”.
Now the question arises that why do we need to study them. And the answer is quite simple.
This is because It significantly reduces the complexity of an underlying problem and also It also reduces the complexity of searching. That is why Sorting algorithm is required before applying Binary Search and it is also used in algorithms implemented in Database.
1.1. Types of Sorting algorithms
Here We’ll explain some of the sorting algorithms so as to give you people some idea about the algorithms.
- Bubble Sort: It initiates by exchanging two elements if they are not according to the desired order, and repeats this mechanism until the array is sorted.
- Insertion Sort: It keeps on scanning the entire collection and when any out of order element is encountered, it inserts that item into its proper place.
- Selection Sort: It find the smallest element in the collection and then put it in proper place and then it swaps it with the element in the first position, it keeps on repeating this action until the array become sorted.
- Quick Sort: It partition the collection of elements on the basis of a pivot value. It divides the array into two segments, first one contains the elements less than or equal to the pivot value and second segment contains the elements greater than pivot value, and then it sort the two segments recursively. And In this tutorial, we’ll discuss this sorting algorithm.
- Merge Sort: It divides the collection in two parts and then sort the parts individually and then merge them.
2. Quick Sort Introduction
Quick sort is a sorting algorithm formulated by Tony Hoare that, on normal, makes O(nlogn) comparisons to sort n items. In the worst case, it makes O(n2) comparisons, though this behavior is extraordinary. Quick sort is ofttimes faster in practise than another O(nlogn) algorithms. Additionally, quick sort's sequential and localized memory references work well with a cache. Quick sort can be implemented as an in-place sort, requiring exclusive O(logn) additional space.
Quick sort is a divide and conquer algorithm which relies on a partition procedure: to partition an array an element called a pivot is selected. All elements smaller than the pivot are moved before it and all greater elements are affected after it. This can be through efficiently in linear period and in-place. The lesser and greater sublists are then recursively sorted. Efficient implementations of quick sort are typically unstable sorts and somewhat complex, but are among the fastest sorting algorithms in activity. Together with its modest O(log n) set activity, quick sort is one of the most popular sorting algorithms and is available in some standard programming libraries. The most complex issue in quick sort is choosing a good pivot element; consistently poor choices of pivots can result in drastically slower O(nË›) performance, if at each step the median is chosen as the pivot then the algorithm works in <br/>. Finding the median however, is an O(n) operation on unsorted lists and thus exacts its own penalization with sorting.
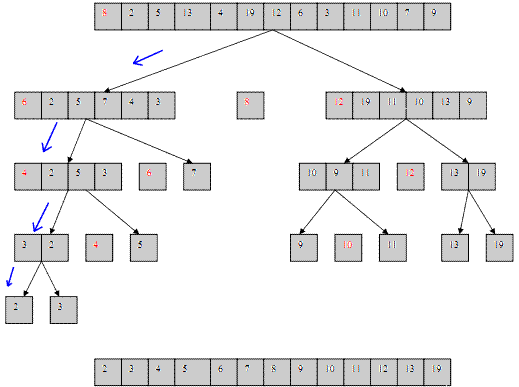

Here We’ll explain briefly Quick Sort
It works by partitioning the array which is given, into two sub-array. Let’s assume that A[p…..r] be the given array and two sub arrays , let’s say S1 is A[p…q] and S2 is A[q+1….r]. Here we divided the elements into the sub-arrays such that every element in S1 is either less than or equal to every element of S2. There is a way of selecting the exact position of partitioning which we’ll explain later. The point, here it is q is called pivot point or value. These two subarrays are then sorted recursively.
3. Quick Sort Algorithm
Know More about Quick Sort Algorithm here
4. Quick Sort Example
Let’s take an example to understand quick sort more precisely.
We have an array namely, A = { 9, 7, 5, 11, 12, 2, 14, 3, 10, 6 {
We need to sort it using quick sort algorithm.
To understand mechanism more clearly, we’ll be using coloured boxes, where the red boxes have been pivots previously and Therefore, these values will not be moved or examined again.
In fig a), the array is unsorted and that is why all the locations are green in colour.
The values inside the boxes are the elements and the values written above are indexes.

p represents the first element and r represents the last element.

In fig b), we took last that is r as the pivot element and q is the symbol we are using for pivot, arranging the elements accordingly. That means, the elements lesser than pivot will be on left side of q and elements greater than q will be on its right side.

In fig c), we sorted the two partitions again taking q as pivot element in each of them and also p and r as first and last elements respectively in both the partitions.

In fig d), we are examining all the elements, leaving the red ones, as explained earlier.


5. Quick Sort pseudocode
{`quicksort(A,p,r)
{
if (p < r)
{
q= partition(A,p,r)
quicksort(A,p,q)
quicksort(A,q+1,r)
}
}
partition(A,p,r){
pi = A[low]
l = low
for a = p+1 to r{
if (A[a] < pi) {
swap(A[a], A[l])
l = l + 1
}
}
swap(pi,A[l])
return (l)
}
`}
6. Quick Sort Code in Java
{`public class quickSort {
protected static int A[];
public void sort(int[] A) {
if (A == null || A.length == 0)
return;
quicksort(A, 0, A.length - 1);
}
public void quicksort(int[] A, int p, int r) {
int pivot = A[p+ (r - p) / 2];
int i = p;
int j = r;
while (i <= j) {
while (A[i] < pivot) {
i++;}
while (A[j] > pivot) {
j--; }
if (i <= j) {
swap(i, j);
i++;
j--;
}
}
if(p < j)
quicksort(A,p,j);
if(i < r)
quicksort(A,i,r);
}
public void swap(int i, int j){
int temp=A[i];
A[i]=A[j];
A[j]=temp;
}
public String toString() {
String s = "";
s += "[" + A[0];
for (int i = 1; i < A.length; i++) {
s += ", " + A[i];
}
s += "]";
return s;
}
`}
7. Quick Sort Code in C
{`#include< stdio.h>
void quicksort(int A[50],int p,int r){
int i, j, pivot, temp;
if(p< r){
pivot=p;
i=p;
j=q;
while(i< j){
while(A[i]<=A [pivot]&&i< r)
i++;
while(A [j]>A [pivot])
j--;
if(i< j){
temp=A [i];
A[i]=A [j];
A[j]=temp;
}
}
temp=A [pivot];
A[pivot]=A [j];
A[j]=temp;
quicksort(A,p,j-1);
quicksort(A,j+1,r);
}
}
int main(){
int i, count, A[50];
printf("How many elements ?: ");
scanf("%d",&count);
printf("Enter %d elements: ", count);
for(i=0;i< count;i++)
scanf("%d",&A[i]);
quicksort(A,0,count-1);
printf(" Sorted elements: ");
for(i=0;i< count;i++)
printf(" %d",A[i]);
return 0;
}
`}
8. Complexity of quick sort
For Worst Case: The time complexity is O(n^2). It happens when the pivot is either the smallest or the largest element. And we explained the complications for that case in earlier section.
For Best Case: It is O(NlogN). In this case the pivot is the median of the array. Here the left and right side is of same size. And in that case, there will be log n partitions and for that we’ll do n comparisons. That is why the complexity is O(NlogN).
Find the best Quick Sort Assignment Help Services with us
Try our determination care now, solution of your problem is righteous a depression departed. Knock any quantify at our 24x7 live supports for any ask. To know about how to proceed, just visit how it Works page at Assignmenthelp.net.
To submit Quick Sort Assignments Click here


