Physics Assignment Help With Potential And kinetic Energies

7.3 Energy in oscillating system: Potential and Kinetic energies

Consider the spring-mass system shown in figure. When the mass is pulled, the spring is elongated. The amount of energy required to elongate the spring through a distance dx is equal to the work done in bringing about this change. It is given by dW = dU = F0 dx, where F0 is the applied force (such as by hand). This force is balanced by the restoring force. That is, its magnitude is same as that of F and we can write F0 = kx. Therefore, the energy required to elongate the spring through a distance x is

... (i)

This energy is stored in the spring in the form of potential energy and is responsible for oscillations of the spring-mass system.

On substituting for the displacement

… (ii)

Note that at t = 0, the potential energy is

… (iii)

As the mass is released, it moves towards the equilibrium position and the potential energy starts changing into kinetic energy (K.E.). The kinetic energy at any time t is given by K.E. = mv2.

K.E. =

= … (iv)

Since

One can also express K.E. in terms of the displacement by writing

K.E. = … (v)

=

= … (vi)

This shows that when an oscillating body passes through the equilibrium position (x =0), its kinetic energy is maximum and equal to

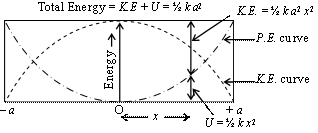
It is thus from the explicit time dependence of equations that in a spring-mass system the mass and the spring alternately exchange energy. Let is consider that the initial phase f = 0. At t = 0, potential energy stored in the spring is maximum and K.E. of the mass is zero. At t = T /4, the potential energy is zero and K.E. is maximum. As the oscillates, energy oscillates from kinetic form to potential form and vice versa. At any instant, the total energy, E, of the oscillator will be sum of both these energies. Hence, from equation, we can write

This means that the total energy remains constant independent of time) and is proportional to the square of the amplitude. As long as there are no dissipative forces like friction, the total mechanical energy will be conserved.

Email Based Assignment Help in Potential And kinetic Energies

We are the leading online Assignment Help provider. Find answers to all of your doubts regarding the Potential And kinetic Energies. Assignmenthelp.net provide homework, Assignment Help to the school, college or university level students. Our expert online tutors are available to help you in Potential And kinetic Energies. Our service is focused on: time delivery, superior quality, creativity and originality.

To submit physics Potential And kinetic Energies assignment Click here

Following are some of the areas in physics Simple Harmonic Motion which we provide help: