Physics Homework Help With Moment Of Inertia Of Continuous Body

Moment Of Inertia Of Continuous Body

For calculating moment of inertia of a continuous body, we first divide the body into suitably chosen infinitesimal elements. The choice depends on symmetry of body. Consider an element of the body at a distance r from the axis of rotation. The moment of inertia of this element about the axis we defined as (dm)r2 and the discrete sum over particles becomes integral over the body:

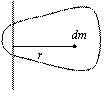
… (vii)

Moment of Inertia for different bodies

1. Moment of inertia of a rod

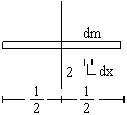
(a) About an axis passing through its centre and perpendicular to its length. Considering a small element of the rod of length dx and mass dm at a distance x from the axis where moment of inertia of continuous body image3

The moment of inertia of this element about the given axis is dI = dm.x2 =

Hence the moment of inertia of whole rod is

I =

(b) About an axis touching the edge of the rod and perpendicular to the length of the rod.

It can be obtained by using the limits from zero to L

where

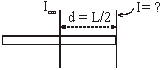
moment of inertia of continuous body image7

I =

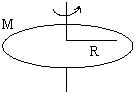
2. Uniform Circular ring:

If M is the mass of the ring with radius R, then moment of inertia about an axis passing through the center of ring perpendicular to its plane can be obtained by

moment-of inertia of continuous body image10

3. Uniform circular Disc:

Uniform circular disc about an axis passing through its centre and perpendicular to its plane. Dividing the disc into a number of concentric rings and considering one ring of radius r and thickness dr. Let due to the mass of the disc and moment of inertia of continuous body image11

(i) given by

The moment of inertia about the given axis of this ring

therefore the moment of inertia of the whole disc is given by

It may be noted that the moment of inertia of a disc and of a ring is independent of their thickness.

Moment of Inertia of Some Common Shaped Bodies

*A Thin Rod* The axis is perpendicular to the rod and passing through its centre. Ic =		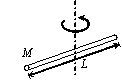*A Thick Rod* The axis is perpendicular to the rod and passing through the centre.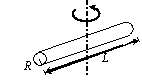
*A Ring* Axis is perpendicular to the plane of the ring		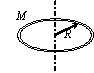*A Hollow Cylinder*
*A Disc* The axis perpendicular to the plane of the disc.		A Solid Cylinder
A thin rod about a perpendicular axis through its end. I =		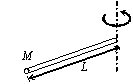A rectangular plate about one edge.
*A Solid Sphere* About its diameter		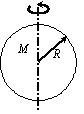*A Hollow Sphere* About its diameter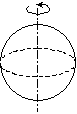
Annular Disc About an axis perpendicular to plane of disc		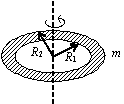Thick Hollow cylinder About axis of the cylinder
A Rectangular Plate Axes lying in the plane of the plate and passing through c.m. 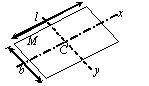> ,		Axis perpendicular to plane and passing through its c.m.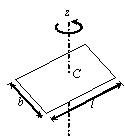

Homework Help For Moment of inertia of continuous body

assignmenthelp.net provides best Online Assignment Help service in Physics for all standards. Our Tutor provide their high quality and optimized Tutorial help to fulfill all kind of need of Students.

To submit Moment of inertia assignment click here.