Statistics Assignment Help With Hypergeometric Distribution

When the population is finite and the sampling is done without replacement, so that the events are stochastically dependent, although random, we obtain hypergeometric distribution. Consider an urn with N balls, M of which are white and N-M are red. Suppose that we draw a sample of n balls at random ( without replacement) from the urn, then the probability of getting k white balls out of n, (k <n) is

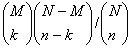
A discrete random variable x is said to follow the hypergeometric distribution if it assumes only non-negative values and its probability mass function is given by

P(X =k) =h(k;N,M,n) = 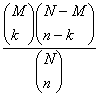k =1,2,….,min(n,M).

= 0 otherwise

5.6.1 Mean and Variance of the Hypergeometric Distribution:

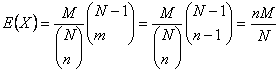
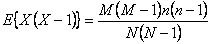
Email Based Homework Help in Hypergeometric Distribution

To submit Hypergeometric Distribution assignment click here.

Following are some of the topics in Theoretical Discrete Distributions in which we provide help: