NPV, IRR capital budgeting tools

The most important capital budgeting tools are:

There are two important measures in order to analyse any investment project:

Net present Value (NPV)
Internal Rate of return (IRR)
Payback period

Out of these three, IRR and NPV are considered the most accurate measures because we know often know the cash outflows, cash inflows and discount rates. So, there is less chances to error. IRR and NPV are the most important capital budgeting benchmark.

Let us understand NPV with an example.

Net Present Value: formula, calculation and examples

Net present value(NPV) is an important capital budgeting tool. NPV (net present value) is the different between the discounted cash inflow (by a chosen discount rate) and discounted cash outflow.

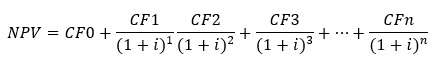
Where CF0, CF1… CFn represent cash flow in the period 0, 1…, n respectively and i represents the risk-adjusted discount rate. If the cash flow is a period represents a cash inflow then we record its value with a positive sign. If there is a cash outflow then its value is recorded with a negative sign in the above formula for NPV calculations. In a standard form of cash flows, typically the CF0 term represents a large cash outflow(recorded as negative value) while all future cash flows are positive and represent cash inflow.

If you are looking for a primer on calculating present value and time value of money calculations, click here

To analyse whether the project is good or bad for buying and selling prospects we use net present value. The positive NPV is interpreted as addition of free cash flows.

Whether in the long run or short run the investors tend to accept the project that has a positive net present value.

There are basically two types of proposals:

Investment decision
Consumption decision

The main assumption is that we should take the decision on them separately while making buying decisions and investment decision proposals. The investor must always consider the positive net present value proposal in all decision-making conditions.

Consider the following example:

XYZ ltd is considering a project whether to buying and selling proposal of a particular project. Following details are given as follows

{`
  Given – cash in hand -$500
  Cost of project - $400
  Cost inflow - $400 + $400*15%= $460
  Interest rate – 10%
  `}

{`
  Buying proposal
  Cash inflow @ 10% = $460/ (1+1.10) = 418.18
  NPV= Cash inflow – Cash outflow
  $418.18 - $400
  $18.18
  `}

Total cost incurred - $500 + $18.18 = $518.18

{`
  Selling proposal
  Cash inflow @ 10% = $460/(1+1.10)= 418.18
  NPV- Cash inflow – Cash outflow
  $418.18 - $400
  $18.18
  `}

So as we invest $18.18 at the rate of 10%, we will get $20 today. And as we invest the cash in hand $500 At the rate of 10% in the bank we will get $550 today.

{`
  Total return of investment - $20 + $550
  = $570
  So it’s good to sell the project today.
  `}

As per the question we conclude that our consumption decision does not influence the investment decision. The principle is called separation of decision. You can make investment decision without the concern of future consumption. In the end, the best is for the client is highest NPV.

Errors in Cash Flows versus Errors in the Cost of Capital

Basically, there are two main sources of error in the calculation of NPV.

Cost of capital
Cash flow amount

Based on these there are two Analysis in the Calculation of NPV.

Scenario Analysis – A scenario analysis means analysing different possible events through different alternative values for each possible outcome. Only an abstract image is projected through this analysis.
Sensitivity analysis – Sensitivity analysis is a study of how the uncertainty in the output of the decision model or system can be attributed to different source of uncertainty in the input.

In the long run the errors in cost of capital (interest rate) error tends to be more harmful as compare to the cash flow error. This is because in the long run the cash flow is affected by the interest rate. So, if there is error in discounted rate it will severely affect the NPV calculation in the long run period.

In the short run the cash flow (inflow) error tends to be more harmful as compare to the cost of capital. This is because in the short run, the cash inflow is considered to be important in the decision-making process rather than the discount rate.

Calculating the Internal Rate of Return (IRR)

Another way of estimation of the project or Capital decision making is IRR.

IRR stands for the internal rate of return. Internal rate of return is the discount rate that makes the net difference between discounted cash outflows and inflows value of the specific project equal to zero. Thus, IRR is the discount rate at which NPV = 0. IRR Rate is an indicator of the returns the project is expected to yield.

IRR is calculated through a formula given below.

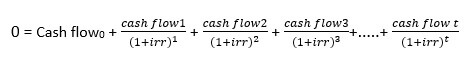
In this formula if the cash flow in a period is a cash outflow then it is taken with a negative sign. If the cash flow in a period is a cash inflow then it is taken with a positive sign.

Here is a solved stepwise example on how to calculate IRR

If the project cost is $100 and the cash inflow in the 1 year is $150. Then computer the Internal Rate of Return for this project.

The IRR can be calculated by setting NPV= 0

{`
  0 = Cashflow0 + cash flow1/(1+irr)¹ 
  0 = (-)100 + 130/(1+irr)¹ 
  Then the IRR = 30%
  `}

NOTE – In the case if there are only two cash flows, the IRR is the final rate of return. Thus, the IRR generalizes the concept of rate of return to multiple cash flows. IRR is the best way of getting the best proposal if there is multiple proposal.

Another name of IRR is also YTM or Yield to Maturity

If the interest rate is lower, this is a positive NPV project. If the interest rate is higher, this is a negative NPV project. IRR can be calculated for both negative and positive cash flows. IRR can also be used to calculate expected returns on stocks or investments, including the yield to maturity on bonds. IRR calculates the yield on an investment and is thus different than net present value (NPV) of an investment.

Can a Project have multiple or no Internal rate of return (IRRs)?

When projects have many positive and many negative cash flows, they can often have multiple internal rates of return. If the cash inflow is same as the cash outflow for the year then the internal rate of return is equal to zero. And IRR can be positive or negative for the same project. While some projects have multiple IRRs, other projects have none. For example, negative or all positive cash flows have no IRR. Example: what is the internal rate of return of a project that yields $10 today and $20 tomorrow (that is, it never demands an investment)? Such a project has no internal rate of return. The NPV formula is never zero, regardless of what the prevailing interest rate is.

When to use IRR as a Capital-Budgeting Rule?

One important reason why IRR is so useful is that it can often substitute for NPV as an investment criterion.

The IRR capital budgeting rule states that if and only if an investment projects IRR (a characteristic of the project cash flows) is above the appropriate discount rate (cost of capital) for the project, then the project should be taken. In this context, the cost of capital is often called the hurdle rate.

Many times, the IRR and NPV gives the same answer of the existing project.

Why we use IRR instead of the NPV investment criterion: NPV vs IRR

Basically, IRR is often quite intuitive and convenient, especially if the project’s cash flow stream implies one unique IRR. IRR is convenient because you can compute it without having looked at financial markets, interest rates, or costs of capital. This is IRR’s most important advantage over NPV: It can be calculated even before we know the appropriate interest rate (cost of capital). IRR can be computed before the cost of capital.

Problems with IRR as a Capital-Budgeting Rule

It is good to use IRR instead of NPV because it is an accurate way of calculating the project’s return. But it is safer to use NPV instead of IRR because NPV tells us about how much value the investment project can add to the firm. IRR is safe to use when there is only one negative cash flow, specifically in the beginning period of analysis. When there is multiple cash inflow and outflow, it is suitable to use NPV method.

Basically, there are two more problems when using IRR that you need to be aware of:

Project comparisons and scale: The major disadvantage of IRR method is that the IRR uses the rate of return in mutually exclusive projects. IRR has no concept of scale.
Cost of capital comparison: The long-term interest rates are often higher than short-term interest rates.

For example, in mid-2002, a 1-year Treasury bond offered a rate of return of 2%, while a 20-year bond offered a rate of return of 6%. Assuming that your project is risk-free. Should we take a risk-free project? There will not be an obvious hurdle rate to compare it to.

The Profitability Index

The profitability index indicates the ratio of discounted cash inflow with the original investment made. It divides the present value of cash inflow with the projected cost of the project. The profitability index can make projects with lower starting costs and scale look more desirable.

The profitability index is calculated by the following formula:

Profitability Index = Present Value ( future cash inflow) )/Initial cost of investment

Let us understand with an example.

If the initial investment of a project is $1000 and the cash inflow discounted @10% are given as follows

Period	1	2	3	4	5
Cash Inflow	50	250	300	500	400

Find the profitability index of the existing project.

Profitability Index = Present Value ( future cash inflow)/Initial cost of investment

{`
  Total of present value of cash inflow - $50+ $250+ $300+ $ 500+ $ 400
  = $ 1500
  Initial cost of investment = $ 1000
  Profitability Index = ( 1500 )/(1000 ) = 1.5 : 1
  `}

A positive-NPV project usually has a profitability index above 1 because the profitability index is meaningful only if there is a standard flow of cash with the first period having cash outflow.

The statements “NPV > 0” and “profitability index > 1” are the same.

The profitability index gives the information of the relative performance of the capital and use of capital. The profitability index values the scale of the project differently. The project with the same NPV is will have different profitability index due to less capital use. It may even be less risky, but this can be deceiving, because their it is not specified the risk of the future cash flows.

Calculating the Payback Period Rule

Basically, the payback period, as suggested by the name, is the time period within which your initial investment is recovered in the form of the cash inflows.

Payback period is of two types:

Normal payback period
Discounted payback period

Payback period = cash ouflow(initial cost of investment)/cash inflow ( discounted value)

Let us understand the concept of Payback Period with an Example

Steven purchase a table costing $2000 and from that every year he is getting a return of $100. Find out the payback period.

Payback period = cash ouflow (initial cost of investment)/cash inflow ( discounted value)

Payback period = $2000/$100
= 20 Year

Advantages of Payback period over NPV and IRR

It helps an investor to get to know in how many year he/she will get the investment back.
Payback period also helps to judge a project’s liquidity to payback the amount borrowed from the market.
Payback period, therefore, helps in decision making for business managers and entrepreneurs.
Helps to determine the NPV of the project. Also determine whether the NPV is positive or negative.

The most common capital budgeting instrument is NPV and IRR for a sound capital decision making.

Online Finance tutors available 24x7 for help with NPV and IRR calculations

Are you looking for reliable and affordable online finance tutors to help you with your finance homework problems related to NPV, IRR, payback period, capital budgeting, valuation or financial modelling homework assignments? Get instant finance homework help from online tutors at AssignmentHelpNet

Sign up now to get online finance homework help